【標準】ある点から引いた接線（三次関数）

🕒 2017/10/21 🔄 2023/05/01

ここでは、ある点から三次関数のグラフに引いた接線の方程式を求める問題を考えます。

📘 目次

ある点から引いた接線

例題

点 $(2,-2)$ から、曲線 $y=x^3-x$ に引いた接線の方程式を求めなさい。

問題によっては、「点 $(2,-2)$ を通り、曲線 $y=x^3-x$ に接する直線の方程式を求めなさい。」となっている場合もありますが、同じことです。曲線上にない点から、その曲線に接線をひいて、その直線の方程式を求める、ということです。

通る点が分かっているので、傾きが分かれば直線の方程式は求められます。しかし、傾きを直接求めるのは難しいです。接線の傾きを求めるには、接点の情報が必要だからです。

そのため、【標準】三次関数の接線の傾きから接線を求めるのときと同じように、「接点の座標を文字で置いて」考えていくことにします。

$f(x)=x^3-x$ とし、この曲線上の点 $(a,f(a))$ について考えてみましょう。この点での接線の傾きは\[ f'(a)=3a^2-1 \]ですね（参考：【基本】整式の導関数）。よって、接線の方程式は、次のようになります（参考：【基本】微分と接線の方程式）。
\begin{eqnarray} y-f(a) &=& f'(a) (x-a) \\[5pt] y &=& (3a^2-1) (x-a) +(a^3-a) \\[5pt] &=& (3a^2-1)x -3a^3+a +a^3-a \\[5pt] &=& (3a^2-1)x -2a^3 \\[5pt] \end{eqnarray}接点の情報があれば、それをもとに接線の方程式がこのように求められます。これがさらに点 $(2,-2)$ を通る、と考えれば、 a 、つまり、接点の x 座標が求められる、というわけですね。

代入してみると
\begin{eqnarray} -2 &=& (3a^2-1)\times 2 -2a^3 \\[5pt] -1 &=& 3a^2-1 -a^3 \\[5pt] a^3-3a^2 &=& 0 \\[5pt] a^2(a-3) &=& 0 \\[5pt] a&=& 0,3 \end{eqnarray}となります。

接線の方程式は先ほど求めたように、\[ y=(3a^2-1)x -2a^3 \]なので、これらの解を代入すればいいですね。 $a=0$ のときは\[ y=-x \]となり、 $a=3$ のときは\[ y=26x-54 \]となります。この2つが求める方程式となります。下のグラフは、縦と横の縮尺を変えています。

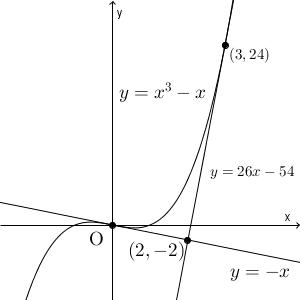
突き抜ける接線

ところで、上の例題で出てきた $y=x^3-x$ と解に出てきた $y=-x$ について、もう一度見てみましょう。

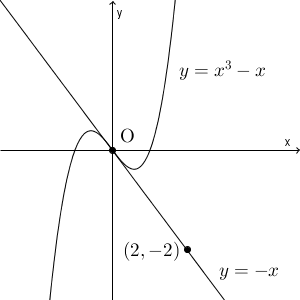
この直線は $(2,-2)$ から引いた接線であり、原点が接点となっています。

微分を学ぶまでは、円と接線、放物線と接線という場面で接線が出てきました。そのときは、接線が円を突き抜けるとか、放物線を突き抜ける、なんてことはありませんでした。

しかし、微分を学んで以降は、接線というのは、【基本】微分と接線の方程式で見たように、定義が少し変わりました。上の関数の原点での接線とは、原点と $(a,f(a))$ とを結んだ直線が、 $a\to 0$ としたときに近づいていく直線、と定義しなおしました。言い換えれば、接点を通り、その点での微分係数と等しい傾きの直線、ということです。実際計算すると、 $f'(0)=-1$ なので、接線の傾きと一致します。

接線の定義が変わった結果、この画像のように、接線が三次関数のグラフを突き抜けているようなものも出てきます。円や放物線のときにはありえませんでしたが、三次関数のグラフの場合は、こういう例もある、ということを知っておきましょう。