【標準】比例や反比例を利用する問題

🕒 2019/06/22 🔄 2023/05/01

ここでは、比例や反比例を利用する問題を見ていきます。

📘 目次

問題文から変域を考える問題

例題1

四角形ABCDは長方形で、 AB=6cm, AD=9cm です。点Pは、点Aを出発して、辺ADの上を毎秒1cmの速さで点Dまで進みます。ここで、点Pが点Aを出発してから $x$ 秒後の三角形ABP の面積を $y\mathrm{cm}^2$ とします。
(1) $x$ の変域を求めなさい。
(2) $y$ を $x$ の式で表しなさい。
(3) $x$ と $y$ の関係を、グラフで表しなさい。

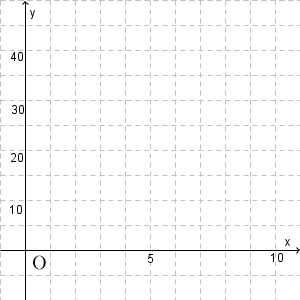
点Pは、点Aを出発して、点Dまでいきます。

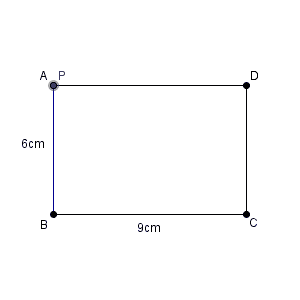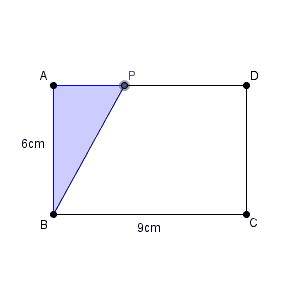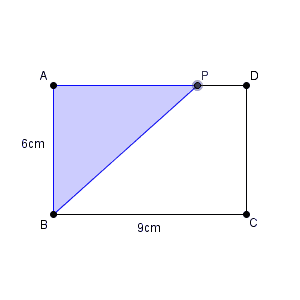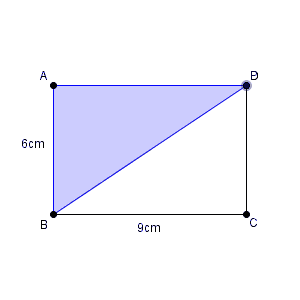
AD=9cmであり、点Pの進む速さは毎秒1cmなので、最大で9秒進みます。これより長くは進めません。一方、出発するときは0秒であり、 $x$ がマイナスになることもありません。よって、 $x$ の変域は、\[ 0\leqq x \leqq 9 \]となります。これが(1)の答えです。

$y$ は三角形ABPの面積です。三角形の面積を求めるには、底辺と高さがわかればいいですね。ABを底辺と考えれば、APが高さを表している、と考えられます。ABの長さは6cmです。APの長さは、点Pが移動した距離なので、 $x$ cmとなります。以上から、\[ y=\dfrac{1}{2}\times 6\times x=3x \]となります。これが(2)の答えです。

$y=3x$ という関係と、 $0\leqq x\leqq 9$ という変域がわかったので、(3)は、これらをもとにグラフをかくだけです。次のようなグラフとなります。

原点と $(5,15)$ とを結ぶ線を引けばいいですね。変域を考慮して、原点から出発して、 $x$ 座標が9までのところで止めるようにします。

現実の問題に応用する場合は、このように、とり得る値が決まっていることがあります。この問題では、(1)で「 $x$ の変域を答えなさい」と言われていますが、問題によっては、書かれていないこともあります。その場合は、自分で気づかないといけません。問題を読んで、 $x$ のとり得る範囲は $0\leqq x\leqq 9$ だな、と気づいて、この範囲でグラフをかかないと正解にはなりません。

歯車の問題

例題2

歯車Aは歯数が16、歯車Bは歯数が30、歯車Cは歯数が $x$ です。歯車Aが15回転したときに、歯車Cが $y$ 回転するとき、 $y$ を $x$ の式で表しなさい。

歯車とは、次のようなものです。

上の歯車が、例えば時計回りに回転したとしましょう。すると、歯がかみ合っているところによって、左の歯車も動き出します。動く向きは、反時計回りです。かみ合っているところが、左上のほうに行こうとするので、左側の歯車には、反時計方向に回る力が加わるからです。

この結果、右下の歯車も回ります。かみ合っているところは、右上の方向に行く力が加わるので、右下の歯車は、時計回りに回転します。歯車は、このようにして、回転を伝えていくためのもので、アナログ時計の中など、いろいろな機械の中で使われています。

歯数とは、歯車のまわりについている、ギザギザの数です。ギザギザの数が同じなら、片方が1回転するとき、もう片方も1回転することはすぐにわかるでしょう。しかし、歯数が違う場合は、少し難しいですね。

仮に、歯数が20の歯車と歯数が10の歯車がかみ合ってたとします。そして、20のほうが1回転するとしましょう。かみ合っているところに注目すると、同じ歯数分だけ回転しないといけないことがわかります。つまり、歯数が20の歯車が1回転するなら、20の歯数だけ回転するので、歯数が10の歯車も同じだけ回転する必要があります。そのため、$20\div 10=2$ 回転することがわかります。

同じ歯数分だけ回転しないといけないので、歯数が少ないと、より多く回転しないといけない、ということなんですね。このことから、歯数と回転数の積は、同じにならないといけないことがわかります。

このことを利用して、この例題を考えてみましょう。歯車A, B, Cの歯数は、それぞれ、16, 30, $x$ でした。歯車の動きを、順番に考えてみましょう。歯車Aが 15回転すると、歯数は $16\times 15=240$ だけ進むので、歯車Bも同じだけ進む必要があります。なので、歯車Bは、 $\dfrac{240}{30}=8$ 回転しないといけないことがわかりますね。

これを受けて、歯車Cがどう動くかを考えましょう。歯車Bがどれだけの歯数分回転するかを考えると、 $30\times 8=240$ となります。この数字は、先ほど出てきた数字と同じですが、よく考えると、これは当たり前です。歯車A, B, Cはそれぞれかみ合っているのだから、回転する歯数は同じになります。つまり、実は歯車Bが何回転するかなんて、どうでもいいんですね。歯車Aが $240$ 分の歯数だけ回転したのだから、その回転が伝わって、歯車Cも $240$ 分の歯数だけ回転することになります。よって、回転数 $y$ は $240$ を $x$ で割って\[ y=\frac{240}{x} \]となることがわかります。

歯車の問題は時々出題されます。どのような動き方をするか、どのように考えるかは、この機会にマスターしておきましょう。