【標準】三角形の重心の座標
ここでは、三角形の重心の座標がどうなるかを考えていきます。結論はきれいな式になります。
三角形の重心の性質
三角形の重心の座標を考える前に、三角形の重心がどのような性質を持っていたか、振り返っておきましょう。【基本】三角形の重心の内容からもわかる通り、重心は、中線を $2:1$ に内分する点なんですね。
これを踏まえて、座標を求めていきましょう。
三角形の重心の座標
下の図のように、三角形 ABC について考えます。 P は BC の中点で、 G を重心とします。
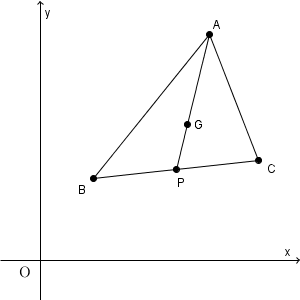
各頂点の座標を $\mathrm{ A }(x_1,y_1)$, $\mathrm{ B }(x_2,y_2)$, $\mathrm{ C }(x_3,y_3)$ とし、重心 G の座標がどうなるかを考えます。
まず、点 P は BC の中点なので、【標準】中点の座標で見たように、座標は\[ \left(\frac{x_2+x_3}{2},\frac{y_2+y_3}{2}\right) \]と求められます。
また、重心 G は AP を $2:1$ に内分する点なので、【基本】平面上での内分点と外分点で見た内容が使えます。 x 座標は
\begin{eqnarray}
\frac{1\cdot x_1+2\cdot \dfrac{x_2+x_3}{2} }{2+1} = \frac{x_1+x_2+x_3}{3}
\end{eqnarray}と求められます。また、 y 座標も同様に計算すれば
\begin{eqnarray}
\frac{y_1+y_2+y_3}{3}
\end{eqnarray}と求めることができます。
まとめると、次のように書くことができます。
よく見ると、3つの座標の平均になっていますね。中点の座標は2つの平均、三角形の重心の座標は3つの平均になっています。きれいで覚えやすいですね。
例えば、 $\mathrm{ A }(1,2)$, $\mathrm{ B }(3,4)$, $\mathrm{ C }(5,6)$ を頂点とする三角形 ABC の重心を求める場合は、\[ \left(\frac{1+3+5}{3}, \frac{2+4+6}{3}\right) = (3,4) \]と計算できるわけなんですね。
おわりに
ここでは、三角形の重心の座標がどのように求められるかを見てきました。3つの頂点の座標の平均を出せば、重心の座標になるんでしたね。結果はきれいなので覚えやすいと思いますが、どのように求めたのかも合わせて覚えておきましょう。





