【標準】ある点に関して対称な点の座標

🕒 2017/07/14 🔄 2023/05/01

ここでは、ある点に関して対称な点の座標を求めます。いくつかの方法で解いてみます。

📘 目次

ある点に関して対称な点の座標

例題

点 $\mathrm{ A }(3,2)$ に関して、点 $\mathrm{ P }(4,-1)$ と対称な点 Q の座標を求めなさい。

まずは、図をかいて考えてみましょう。

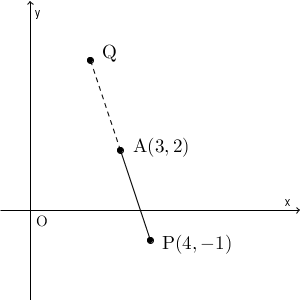
図から、「P から A に移動するのと同じ距離だけ、 A から移動すればいい」ことがわかりますね。左に $1$ 、上に $3$ 移動すれば P から A に移動できるので、 A を出発点にして同じだけ移動することを考えて\[ (3-1,2+3)=(2,5) \]が Q の座標になることがわかります。

中点と考える方法

対称な点の座標を求める方法は他にもあります。【標準】中点の座標で見た内容を使ってみましょう。

「対称な点」と見るのではなく、「PQ の中点が A である」という見方をしてみましょう。対称な点なので、こうした見方が成り立ちますね。

$\mathrm{ Q }(x,y)$ とすると、中点の座標に関する式を作れば
\begin{eqnarray} \frac{4+x}{2} &=& 3 \\[5pt] x &=& 2 \\[5pt] \end{eqnarray}と \begin{eqnarray} \frac{-1+y}{2} &=& 2 \\[5pt] y &=& 5 \\[5pt] \end{eqnarray}となるので、 Q の座標は $(2,5)$ と求められます。

教科書や参考書で、よく紹介される解き方です。

外分点と考える方法

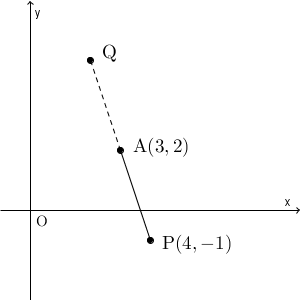
先ほどは「PQ の中点が A である」と考えましたが、「Q は、線分 AP を $1:2$ に外分する点である」と考えることもできます。

こう考えると、【基本】平面上での内分点と外分点で見た内容から、次のようにして Q の座標を、より直接的に求めることができるようになります。
\begin{eqnarray} & & \left(\frac{(-1)\cdot 4+2\cdot 3}{2-1}, \frac{(-1)\cdot (-1)+2\cdot 2}{2-1}\right) \\[5pt] &=& \left(-4+6, 1+4\right) \\[5pt] &=& (2, 5) \\[5pt] \end{eqnarray}このように求めることもできます。

それぞれの解き方の関係

上では3つの方法を紹介しました。当たり前ですが、どの方法でも答えは同じになります。また、本質的にはどれも同じ計算をしています。

一般的な例で考えてみましょう。 $\mathrm{ A }(a,b)$, $\mathrm{ P }(x_1,y_2)$ とし、点 A に関して、点 P に対称な点 Q の座標 $(x_2,y_2)$ を求めてみましょう。

1つ目の方法では、まず P から A への移動について考えます。右に $a-x_1$ 、上に $b-y_1$ だけ移動すればいいですね。 A を基準に同じだけ移動すれば
\begin{eqnarray} (x_2,y_2) &=& (a+a-x_1,b+b-y_1) \\[5pt] &=& (2a-x_1,2b-y_1) \end{eqnarray}が得られます。

2つ目の方法では、次の関係を使います。\[ \left(\frac{x_1+x_2}{2},\frac{y_1+y_2}{2}\right)=(a,b) \]PQ の中点が A である、ということを式にしたわけですね。両辺を2倍して P の座標を移行すれば、\[ (x_2,y_2)=(2a-x_1,2b-y_1) \]が得られます。1つ目の方法と同じ式が出てきますね。

3つ目の方法では、「Q は、線分 AP を $1:2$ に外分する点である」と考えて、より直接的に次のように求めます。
\begin{eqnarray} (x_2,y_2) &=& \left(\frac{(-1)\cdot x_1+2\cdot a}{2-1}, \frac{(-1)\cdot y_1+2\cdot b}{2-1}\right) \\[5pt] &=& (2a-x_1, 2b-y_1) \\[5pt] \end{eqnarray}これは、1つ目の方法、2つ目の方法で得られた式が、直接導かれていることがわかります。

どれで解いても同じですが、いろいろな見方、解き方ができるようになっておいた方がいいと思います。