【標準】関数の連続性

ここでは、極限で表された関数の連続性を調べる問題を考えます。

関数の連続性を調べる1

【基本】連続関数で見たように、今まで学んだことのある関数は、ほとんどが連続関数なので、そのままの形で連続性を調べることはほとんどありません。そこで、この例題のように極限で表された関数を使って出題されることがあります。

分子にも分母にも $x^n$ に関連するものがありますが、 $n\to\infty$ としたときの挙動は、 $x$ の値によって違うのでした（参考：【基本】等比数列の極限）。場合分けをして考えていきましょう。

まず、 $|x|\lt 1$ のときを考えましょう。このとき、 $n\to \infty$ とすると、 $x^n\to 0$ となります。よって、\[ f(x)=\frac{0+1}{0+2}=\frac{1}{2} \]となります。

$x=1$ のときは、そのまま代入して\[ f(x)=\frac{1+1}{1+2}=\frac{2}{3} \]となります。

$x=-1$ のときは、\[ f(x)=\lim_{n\to\infty}\frac{(-1)^{n+1}+1}{(-1)^n+2} \]となります。 $n$ が偶数のときは\[ f(x)=\frac{-1+1}{1+2}=0 \]であり、奇数のときは\[ f(x)=\frac{1+1}{-1+2}=2 \]なので、振動します。よって、収束しません。

最後に、 $|x|\gt 1$ のときです。このときは、分子も分母も発散するので、両方を $x^n$ で割って考えましょう。\[ \lim_{n\to\infty}\frac{x+\frac{1}{x^n} }{1+\frac{2}{x^n} } \]ここで、 $\dfrac{1}{x^n}$ の部分は $0$ に収束するため、\[f(x)=x\]となります。

以上から、 $f(x)$ は、 $|x|\lt 1$ のときは $\dfrac{1}{2}$ 、 $x=1$ のときは $\dfrac{2}{3}$ 、 $|x|\gt 1$ のときは $x$ となり、 $x=-1$ は定義域に含まれないことがわかります。グラフは次のようになります。

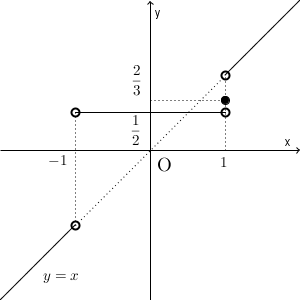
よって、 $f(x)$ は、 $x\ne \pm 1$ で連続、 $x=1$ で不連続であることがわかります。

関数の連続性を調べる2

今度は無限等比級数ですが、これも $x$ の値によって、収束するか、発散するかが異なります。【基本】無限等比級数や【標準】無限等比級数の収束条件で見た内容です。場合分けをして考えていきましょう。

まず、初項が $0$ なら和は常に $0$ です。初項は $x$ なので、 $x=0$ のときは、\[ f(x)=0 \]となります。

次に、 $x\ne 0$ のときを考えましょう。公比は $\dfrac{1}{1-x}$ です。無限等比級数が収束するのは、公比の絶対値が $1$ 未満のときなので、
\begin{eqnarray} \left| \frac{1}{1-x} \right| &\lt& 1 \\[5pt] |x-1| &\gt& 1 \\[5pt] \end{eqnarray}となり、 $x\gt 2, x\lt 0$ となります。また、このときの極限値は、初項 $a$ と公比 $r$ を使って、 $\dfrac{a}{1-r}$ と書けるので、 \begin{eqnarray} x\times \frac{1}{1-\frac{1}{1-x} } &=& x\times \frac{1-x}{1-x-1} \\[5pt] &=& x-1 \end{eqnarray}となります。

以上から、 $f(x)$ は、 $x=0$ のときは $0$ 、 $x\gt 2, x\lt 0$ のときは $x-1$ であり、他の値は定義域に含まれません。グラフは次のようになります。

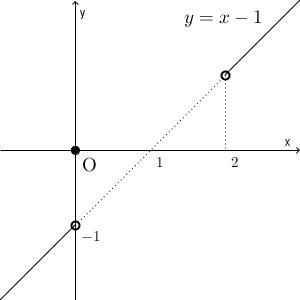
よって、 $f(x)$ は、 $x\gt 2, x\lt 0$ で連続であり、 $x=0$ で不連続であることがわかります。

おわりに

ここでは、極限で表された関数の連続性を調べる問題を見ました。

等比数列や無限等比級数は、公比の値によって、極限の状況が急に変わります。例えば、 $r^n$ の場合、 $|r|\lt 1$ なら $0$ に、 $r=1$ なら $1$ に収束するため、極限は不連続になります。例題1のように、極限を考える前は連続関数でも、極限をとっても連続関数になるとは限りません。極限をとると不連続になることがある、ということは、よく理解しておきましょう。