【標準】空間における2直線のなす角
ここでは、空間における2直線のなす角を求める問題を見ていきます。
例題
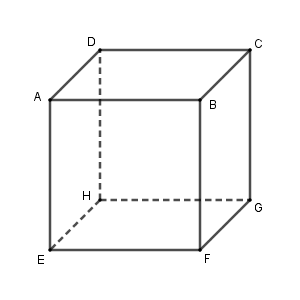
(1) $\mathrm{AE}$ と $\mathrm{DG}$
(2) $\mathrm{AH}$ と $\mathrm{CD}$
(3) $\mathrm{CF}$ と $\mathrm{EG}$
では、(1)を考えてみます。
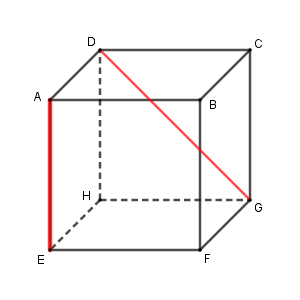
$\mathrm{AE}$ と $\mathrm{DG}$ はねじれの位置にあるので、交わるように平行移動してからなす角を考えます(参考:【基本】空間における2直線の位置関係)。
平行移動の仕方はいろいろありますが、ここでは、 $\mathrm{DG}$ を $\mathrm{AF}$ に移動することにしましょう。

こうすると、三角形 $\mathrm{AEF}$ が直角二等辺三角形であることから、2直線のなす角は $45^{\circ}$ と求められます。
例題の2

(1) $\mathrm{AE}$ と $\mathrm{DG}$
(2) $\mathrm{AH}$ と $\mathrm{CD}$
(3) $\mathrm{CF}$ と $\mathrm{EG}$
次に(2)を考えます。
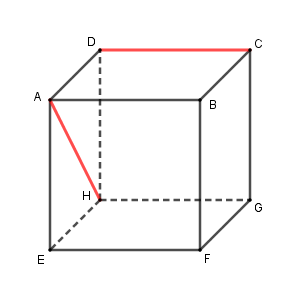
$\mathrm{AH}$ と $\mathrm{CD}$ は交わらないので、これも平行移動をして考えます。 $\mathrm{CD}$ を $\mathrm{GH}$ に平行移動します。
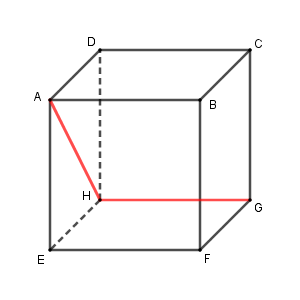
こうすると、 $\angle \mathrm{AHG}$ は $90^{\circ}$ になります。その理由は、 $\mathrm{GH}$ が $\mathrm{DH}$ にも $\mathrm{EH}$ にも垂直であることから、 $\mathrm{GH}$ が平面 $\mathrm{AEHD}$ と垂直であるためです(【基本】空間における直線と平面の位置関係)。 $\mathrm{AH}$ は平面 $\mathrm{AEHD}$ 上の直線なので、 $\mathrm{AH\perp GH}$ となります。
なので、$\mathrm{AH}$ と $\mathrm{CD}$ のなす角は $90^{\circ}$ と求められます。
例題の3

(1) $\mathrm{AE}$ と $\mathrm{DG}$
(2) $\mathrm{AH}$ と $\mathrm{CD}$
(3) $\mathrm{CF}$ と $\mathrm{EG}$
最後に(3)を考えます。
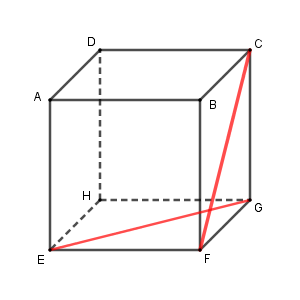
$\mathrm{CF}$ と $\mathrm{EG}$ は交わらないので、これも平行移動します。 $\mathrm{EG}$ を $\mathrm{AC}$ に平行移動しましょう。

今回は、平行移動をしてもまだ角度がわかりづらいですね。角度を考えるために、さらにもうステップ、考えが必要になります。
この2辺を含む、次のような三角形を考えてみます。
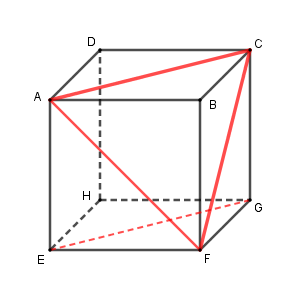
こうすると、三角形 $\mathrm{ACF}$ の各辺は立方体の1辺の長さの $\sqrt{2}$ 倍なので、正三角形であることがわかります。つまり、 $\angle \mathrm{ACF}=60^{\circ}$ です。
こうして、$\mathrm{CF}$ と $\mathrm{EG}$ のなす角は $60^{\circ}$ と求められます。
おわりに
ここでは、空間における2直線のなす角を求める問題を見ました。2直線が交わるように平行移動をするだけでなく、そこからさらに角度を求めるための工夫が必要となる場合もあります。





