【発展】直角三角形の面積とsin2θ

🕒 2016/09/25 🔄 2023/05/01

ここでは、円に内接する直角三角形の面積を考えると、 $\sin2\theta$ を求めることができる、という話をします。 $2\theta$ の三角比は将来詳しく見るのですが、 $2\theta$ が鋭角の場合の $\sin$ は現時点でも求めることができるので、ここで紹介しておきます。

📘 目次

直角三角形の面積1

$\mathrm{ AB }=2$, $\angle \mathrm{ C }=90^{\circ}$ の直角三角形を考えます。また、 $\angle \mathrm{ B } = \theta$ とし、 $2\theta \lt 90^{\circ}$ とします。

この三角形の面積を計算すると、次のようになります。
\begin{eqnarray} \frac{1}{2} \times \mathrm{ AC } \times \mathrm{ BC } &=& \frac{1}{2} \times 2\sin\theta \times 2\cos\theta \\ &=& 2\sin\theta \cos\theta \\ \end{eqnarray}

直角三角形の面積2

さて、上の直角三角形の向きを変え、 AB を直径とする半円をかいてみます。中心を O とします。

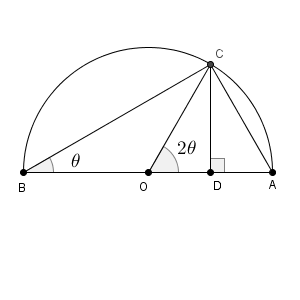
すると、 $\angle \mathrm{ COA }=2\theta$ となりますね。また、 C から AB に下した垂線の足を D とします。

この三角形の面積を出すときに、 $\mathrm{ AB }=2$ を底辺だと考えると、高さは $\mathrm{ CD }=\mathrm{ CO } \times \sin 2\theta$ と書くことができます。CO は半径なので、 $\mathrm{ CO }=1$ ですね。よって、この直角三角形の面積は、次のように書くこともできます。
\begin{eqnarray} \frac{1}{2} \times 2 \times \sin 2\theta = \sin 2\theta \end{eqnarray}

この2つの結果から、\[ \sin 2\theta = 2\sin\theta\cos\theta \]と求めることができます。当たり前ですが、【発展】ひし形の面積とsin2θで求めた式と同じですね。

別の見方

同じ図を見てもう一度考えてみます。今度は、面積ではなく CD の長さに着目してみましょう。

$\mathrm{ AB }=2$ が直径なので、$\mathrm{ CO }=1$ だから、 $\triangle \mathrm{ CDO }$ で考えると、 $\mathrm{ CD }=\sin 2\theta$ と書けます。

また、 $\triangle \mathrm{ ABC }$ で考えると $\mathrm{ BC }=2\cos\theta$ となり、 $\triangle \mathrm{ BCD }$ で考えると次のようになります。
\begin{eqnarray} \mathrm{ CD } &=& \mathrm{ BC }\sin\theta \\ &=& 2\cos\theta\sin\theta \\ \end{eqnarray}このことからも、 $\sin 2\theta = 2\sin\theta\cos\theta$ を導くことができます。