【導入】行列の積と食塩水、あるいは、なぜ行列の積はあんなにめんどくさいのか

🕒 2018/10/01 🔄 2023/05/01

ここでは、行列同士の積を理解するために、食塩水（というか水）を入れ替える問題を考えていきましょう。

📘 目次

水を入れ替える問題

【導入】行列とつるかめ算では、中学入試の問題などでよく出題される「つるかめ算」を用いて行列について考えました。他にも中学入試でよく出題されるタイプとして「食塩水の問題」がありますが、ここでは、その「食塩水の問題」を使って、行列の積（どちらも正方形タイプの行列の積）について見ていきましょう。ただ、中学入試の対策をするのがメインではないので、食塩水の代わりにもっと単純な「水を入れ替える問題」を使うことにしましょう。

例題

コップ X, Y に、それぞれ、水が $x$ グラム、 $y$ グラムずつ入っているとします。ここで、2つの操作を考えます。
　操作１：コップ X にある液体の半分をコップ Y に移す
　操作２：コップ Y にある液体の半分をコップ X に移す
操作１、操作２を順番に行った後、コップ X, Y にはそれぞれどれだけの水が入っていますか。

例えば、X, Y に 120g, 80g の水が入っていたとしましょう。操作１によって、60g の水が X から Y に移るので、操作１の後では、 60g, 140g となります。また、さらに操作２によって、今度は 70g の水が Y から X に移るので、 130g, 70g となります。

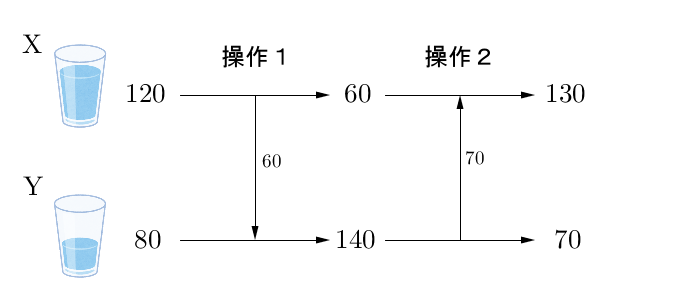
これを一般的な状況で考えましょう。操作１によって、 $\dfrac{1}{2}x$ の水が移るので、操作１の後では、水の重さはそれぞれ\[ \frac{1}{2}x,\ \frac{1}{2}x+y \]となります。また、操作２によって、 Y の半分が移動するので、操作２の後の X の水の重さは、\[ \frac{1}{2}x+\frac{1}{2}\left(\frac{1}{2}x+y\right)=\frac{3}{4}x+\frac{1}{2}y \]であり、 Y は、\[ \frac{1}{4}x+\frac{1}{2}y \]となります。よって、これらが答えです。

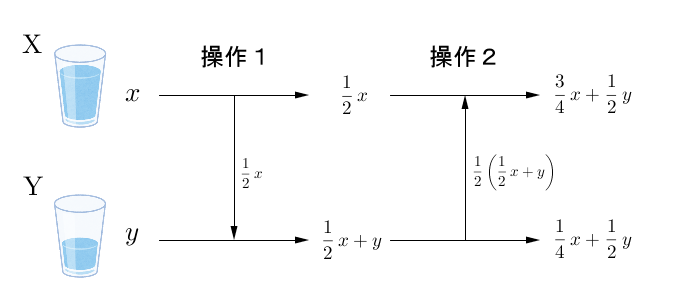
変換を行列で表してみよう

さて、先ほどの内容を、【導入】行列とつるかめ算にならって、各操作を、行列を用いて表してみることにしましょう。

コップ X, Y に入っている水の重さを、次のような行列で表してみます。
\begin{pmatrix} x \\ y \end{pmatrix}これが、操作１によって、次のように変わるのでしたね。 \begin{pmatrix} \frac{1}{2}x \\ \frac{1}{2}x+y \end{pmatrix}このように変換する行列はどのようになるでしょうか。【導入】行列とつるかめ算で見た通り、 \begin{eqnarray} \begin{pmatrix} \diamondsuit & \heartsuit \\ \clubsuit & \spadesuit \end{pmatrix}\begin{pmatrix} x \\ y \end{pmatrix} =\begin{pmatrix} \diamondsuit x +\heartsuit y \\ \clubsuit x +\spadesuit y \end{pmatrix} \end{eqnarray}となることを考えると、次のような行列になることがわかるでしょう。 \begin{pmatrix} \frac{1}{2} & 0 \\ \frac{1}{2} & 1 \end{pmatrix}これが、操作１に対応する行列となります。

同様にして、操作２も行列で書いてみましょう。操作２について考えるときに、操作１の後の結果を使ってもいいのですが、ちょっと式がごちゃっとなっていて考えづらいですね。一度、操作１の結果のことは忘れてみましょう。一番初めの状態
\begin{pmatrix} x \\ y \end{pmatrix}が、操作２によって、どう変わるかを考えてみましょう。そうすると、 Y の半分を X に足せばいいのだから \begin{pmatrix} x+\frac{1}{2}y \\ \frac{1}{2}y \end{pmatrix}となることがわかります。このように変換される行列を考えると \begin{pmatrix} 1 & \frac{1}{2} \\ 0 & \frac{1}{2} \end{pmatrix}となります。

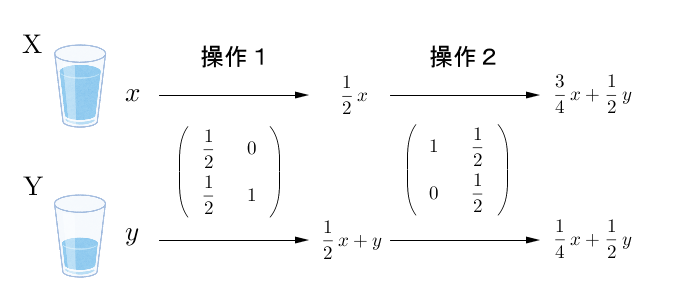
実際に、操作１の後の結果に対して、操作２の変換を計算してみると
\begin{eqnarray} & & \begin{pmatrix} 1 & \frac{1}{2} \\ 0 & \frac{1}{2} \end{pmatrix} \begin{pmatrix} \frac{1}{2}x \\ \frac{1}{2}x+y \end{pmatrix} \\[5pt] &=& \begin{pmatrix} \frac{1}{2}x+\frac{1}{2}\left(\frac{1}{2}x+y\right) \\ \frac{1}{2}\left(\frac{1}{2}x+y\right) \end{pmatrix} \\[5pt] &=& \begin{pmatrix} \frac{3}{4}x+\frac{1}{2}y \\ \frac{1}{4}x+\frac{1}{2}y \end{pmatrix} \end{eqnarray}となり、たしかに、先ほどの例題で見た答えが出てきました。また、例題を解く途中で出てきた式が、行列の中でも出てきましたね。

行列の積はどう定義するのが自然か

さて、先ほどの行列表現を使って、水の問題をもう一度考え直してみましょう。コップ X の半分を Y に移す操作１によって水の重さが変わる様子は、次のように表すことができます。
\begin{eqnarray} \begin{pmatrix} \frac{1}{2} & 0 \\ \frac{1}{2} & 1 \end{pmatrix} \begin{pmatrix} x \\ y \end{pmatrix} &=& \begin{pmatrix} \frac{1}{2}x \\ \frac{1}{2}x+y \end{pmatrix} \end{eqnarray}さらに、この操作１の結果に対して、コップ Y の半分を X に移す操作２によって水の重さが変わる様子は、次のように書けます。 \begin{eqnarray} \begin{pmatrix} 1 & \frac{1}{2} \\ 0 & \frac{1}{2} \end{pmatrix} \begin{pmatrix} \frac{1}{2}x \\ \frac{1}{2}x+y \end{pmatrix} &=& \begin{pmatrix} \frac{3}{4}x+\frac{1}{2}y \\ \frac{1}{4}x+\frac{1}{2}y \end{pmatrix} \end{eqnarray}これにより、最終的な水の重さが得られます。

ここで、1つ目の式を2つ目に代入すれば、次のようになります。
\begin{eqnarray} \begin{pmatrix} 1 & \frac{1}{2} \\ 0 & \frac{1}{2} \end{pmatrix} \begin{pmatrix} \frac{1}{2} & 0 \\ \frac{1}{2} & 1 \end{pmatrix} \begin{pmatrix} x \\ y \end{pmatrix} &=& \begin{pmatrix} \frac{3}{4}x+\frac{1}{2}y \\ \frac{1}{4}x+\frac{1}{2}y \end{pmatrix} \end{eqnarray}ここまでは、 $x,y$ が操作１でどうなって、操作２でどうなるかを計算してきましたが、上の式において、左辺の左側から（正方形の形をした2つの行列の方から）計算する方法があってもいいでしょう。この計算方法はまだ説明していませんが、結果が右辺の通りになることから考えると、 \begin{eqnarray} \begin{pmatrix} 1 & \frac{1}{2} \\ 0 & \frac{1}{2} \end{pmatrix} \begin{pmatrix} \frac{1}{2} & 0 \\ \frac{1}{2} & 1 \end{pmatrix} &=& \begin{pmatrix} \frac{3}{4} & \frac{1}{2} \\ \frac{1}{4} & \frac{1}{2} \end{pmatrix} \end{eqnarray}が成り立つべきだと考えられます。【導入】行列とつるかめ算で見たように、左側の行列は横に、右側の行列は縦にかけて足し合わせていたことも踏まえ、上の式が成り立つようにするには、次のように定義するのが自然です。 \begin{eqnarray} \begin{pmatrix} \diamondsuit & \heartsuit \\ \clubsuit & \spadesuit \end{pmatrix} \begin{pmatrix} \triangle & \square \\ \blacktriangle & \blacksquare \end{pmatrix} = \begin{pmatrix} \diamondsuit\triangle+\heartsuit\blacktriangle & \diamondsuit\square +\heartsuit\blacksquare \\ \clubsuit \triangle+\spadesuit \blacktriangle & \clubsuit \square +\spadesuit \blacksquare \end{pmatrix} \end{eqnarray}複雑ですね。左辺の左側の行列と右辺とを見ると、掛ける前後で、1行目の白文字同士、2行目の黒文字同士とが対応しています。ただ、左辺の右側の行列は、白文字・黒文字の対応はありません。そうではなく、1列目の三角同士、2列目の四角同士が掛けた前後で対応しています。また、2列目の四角の部分がなければ、【導入】行列とつるかめ算で出てきた内容そのままであることにも注意しましょう。

掛ける前と掛けた後でどう対応するか、動きをつけてみると次のようになります。

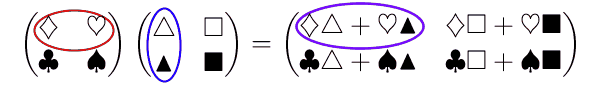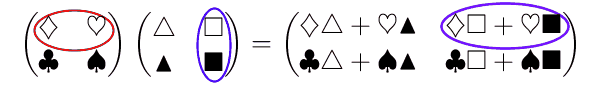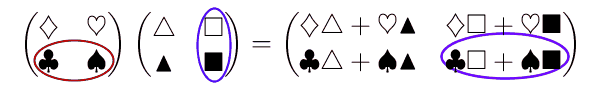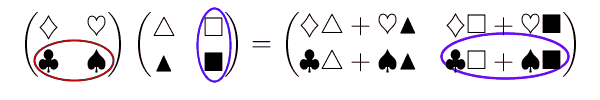
このように定義すれば、先ほどの行列は次のように計算でき、たしかに「成り立つべきだ」と思っていた式が成り立つことがわかります。
\begin{eqnarray} & & \begin{pmatrix} 1 & \frac{1}{2} \\ 0 & \frac{1}{2} \end{pmatrix} \begin{pmatrix} \frac{1}{2} & 0 \\ \frac{1}{2} & 1 \end{pmatrix} \\[5pt] &=& \begin{pmatrix} \frac{1}{2}+\frac{1}{4} & 0+\frac{1}{2} \\ 0+\frac{1}{4} & 0+\frac{1}{2} \end{pmatrix} \\[5pt] &=& \begin{pmatrix} \frac{3}{4} & \frac{1}{2} \\ \frac{1}{4} & \frac{1}{2} \end{pmatrix} \end{eqnarray}

それにしても、行列の掛け算は複雑ですね。はじめて見たら「なんじゃこりゃ」と思う人がほとんどでしょう。「左上同士、右上同士…、と掛けていけばシンプルでいいのになぁ」と思うかもしれません。

しかし、ここまでで見てきたことからもわかる通り、行列の積は、2つの変換（操作１と操作２）を矛盾なく合成できるような定義になっています。これにより、複数の変換の合成は、行列の積を考えることに対応します。値がどのように変わっていくかを見るよりも、変換の合成、行列の積を考えた方がわかりやすくなる場面もあり、そのような例は行列を学んでいく上で、見て行くことになります（行列の n 乗など）。

行列の積は、計算が簡単になることよりも、変換の合成がうまく行える方を優先して、定義に採用しています。分数の足し算も、これに似た決まり方になってる、と言えるでしょう。

分数の足し算は、形だけから考えれば、分母同士・分子同士を出す方が簡単です。しかし、そうしてしまうと、分母・分子に同じ数を掛けても値が変わらない（1/2=2/4, 1/3=2/6 など）という構造が壊れてしまいます。

通分をして計算する方法は、計算が簡単かどうかよりも、分数の持っている性質に整合的であることを優先した定義になっています。行列の積も、行列の持っている性質（変換を表す）に整合的な内容で定義されています。

行列の積の順番を変えると答えが変わってしまうかもしれない

冒頭の問題では、2つのコップの X, Y の水を入れ替えました。まず、 X の半分を Y に、次に Y の半分を X に移動すると、最初に 120, 80 あった水は、130, 70 に変化します。

ここで、入れ替える順番を変えてみましょう。先に、操作２（Y の半分を X に移動）をしてみましょう。最初に、水が 120, 80 あったとすると、この操作で 160, 40 になります。続いて、操作１（X の半分を Y に移動）によって、80, 120 となります。結果が変わってしまいました。

これを行列で表現するとどうなるでしょうか。操作１と操作２に対応する行列を使って書けば、それぞれ次のようになります。1行目が「操作１⇒操作２の場合」、2行目が「操作２⇒操作１の場合」に該当します。
\begin{eqnarray} & & \begin{pmatrix} 1 & \frac{1}{2} \\ 0 & \frac{1}{2} \end{pmatrix} \begin{pmatrix} \frac{1}{2} & 0 \\ \frac{1}{2} & 1 \end{pmatrix} &=& \begin{pmatrix} \frac{3}{4} & \frac{1}{2} \\ \frac{1}{4} & \frac{1}{2} \end{pmatrix} \\[5pt] & & \begin{pmatrix} \frac{1}{2} & 0 \\ \frac{1}{2} & 1 \end{pmatrix} \begin{pmatrix} 1 & \frac{1}{2} \\ 0 & \frac{1}{2} \end{pmatrix} &=& \begin{pmatrix} \frac{1}{2} & \frac{1}{4} \\ \frac{1}{2} & \frac{3}{4} \end{pmatrix} \end{eqnarray}1行目と2行目の結果は異なっていますね。このように、行列の積は、順番を変えると答えが変わってしまう場合があります（たまたま同じになることもあります）。普通の数の計算と大きく異なる点なので、注意しましょう。