【導入】行列のn乗と水の入れ替えと借金

ここでは、水の入れ替え問題を通じて、行列のn 乗の計算について見ていきます。

水の入れ替え問題の設定

【導入】行列の積と食塩水、あるいは、なぜ行列の積はあんなにめんどくさいのかで見た、水の入れ替え問題をもう一度考えてみます。どういう問題だったか、設定を振り返っておきましょう。

2つの水の入ったコップ X, Y に対して、2つの操作を考えるのでした。操作１は、「コップ X の水の半分を Y に移す」、操作２は、「コップ Y の水の半分を X に移す」という内容です。もとのコップの水の量を、それぞれ $x,y$ とすると、操作１と操作２を行った後の水の量は、それぞれ、\[ \frac{3}{4}x+\frac{1}{2}y,\ \frac{1}{4}x+\frac{1}{2}y \]となるのでした。

この一連の操作による、水の量の変化を行列で表すと、上のリンクで見た通り、
\begin{eqnarray} \begin{pmatrix} \frac{3}{4} & \frac{1}{2} \\ \frac{1}{4} & \frac{1}{2} \end{pmatrix} \begin{pmatrix} x \\ y \end{pmatrix} &=& \begin{pmatrix} \frac{3}{4}x+\frac{1}{2}y \\ \frac{1}{4}x+\frac{1}{2}y \end{pmatrix} \end{eqnarray}となります。以下では、この「操作１の後に操作２を行うこと」を1セットで考え、単純に「（水の入れ替え）操作」と呼ぶことにしましょう。

水を入れ替えまくる

ここからは、この水の入れ替え操作を何度も何度も行うと、水の量はどうなるかを考えていくことにします。まずは、具体例で考えてみましょう。はじめの水の重さが、 $(x,y)=(100,80)$ の場合を考えてみます。1セットの操作で、
\begin{eqnarray} \begin{pmatrix} \frac{3}{4} & \frac{1}{2} \\ \frac{1}{4} & \frac{1}{2} \end{pmatrix} \begin{pmatrix} x \\ y \end{pmatrix} &=& \begin{pmatrix} \frac{3}{4}x+\frac{1}{2}y \\ \frac{1}{4}x+\frac{1}{2}y \end{pmatrix} \end{eqnarray}となるのだから、 $(x,y)=(100,80)$ を代入して計算すると、1回目の操作の後では $(115,65)$ となることがわかります（もちろん、操作１と操作２に分けて考えても同じ結果になります）。以下、繰り返し計算して、水の重さがどう変化していくかを図示すると下の通りとなります。

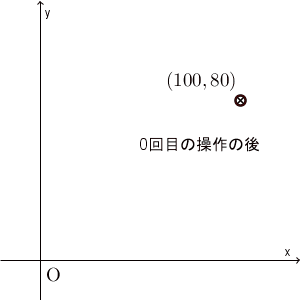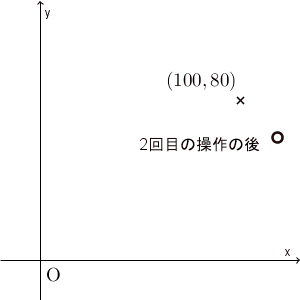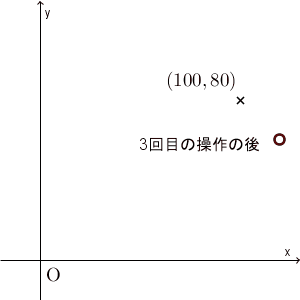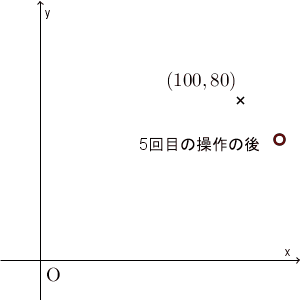
0回目（＝初期状態）の $(100,80)$ から、1回目の後には $(115,65)$ に移ります。ここでは5回の操作しか行っていませんが、ある点に近づいて行ってることがわかります。

上のように図で見る分にはいいのですが、これらを計算で考えていくのは大変です。1回目の後は $(115,65)$ でしたが、2回目の計算では分数やら掛け算・足し算やらが出てきて計算がめんどくさくなります。3回目以降も分数が残って、計算はどんどん複雑になります。

具体的な数字ではなく、文字のまま計算してもやはり大変です。上の式の右辺にあらわれた $\dfrac{3}{4}x+\dfrac{1}{2}y$ と $\dfrac{1}{4}x+\dfrac{1}{2}y$ を左辺の $x,y$ に代入して計算することを考えれば、大変さがわかるでしょう。

状態がどう変わっていくか、を直接順番に計算していくのは、厳しそうです。どういう状態に近づいていくかを直接計算した結果から予想して求めるのは、さらに絶望的だと言えるでしょう。

近づくとしたらどこに近づくだろうか

先ほどは、水の入れ替えを何度も繰り返すとどうなるかを考えようとしましたが、直接計算していくのは厳しそうだ、ということがわかりました。ただ、 $(x,y)=(100,80)$ から始めると、どこかの点（どこかの状態）に近づいていくようだ、ということのがわかります。この点について、考えてみましょう。

もし、ある値に近づくと仮定すれば、おそらく、最終的には、「水の入れ替え操作によって、水の量が変わらない」という状況になっているのではないか、と考えられます。そこで均衡状態となるのでしょう。もし、操作の前後で水の量がそれぞれ変わらないとすると
\begin{eqnarray} \left\{ \begin{array}{l} \frac{3}{4}x+\frac{1}{2}y = x \\ \frac{1}{4}x+\frac{1}{2}y = y \end{array} \right. \end{eqnarray}が成り立つはずです。これを解けば、どちらの式からも\[ x=2y \]という関係式が得られます。例えば、 $(x,y)=(120,60)$ とすると、操作１によって、 $60,120$ となり、操作２によって、 $120,60$ となるため、たしかに値は変わりません。なので、 $x=2y$ の関係式が成り立つ場合、言い換えれば、コップ X の水がコップ Y の水の2倍であれば、何度入れ替え操作を行っても、水の量は変わらないので、初期状態のままであることがわかります。

$(x,y)=(100,80)$ から始めた場合でも、ある状態に近づいていくとすれば、水の量が $2:1$ となる状態に近づくのではないか、と考えられます。水を入れ替えても水の合計は $100+80=180$ で変わらないため、最終的に、水の重さは、 $120,60$ になると予想できます。

実際、先ほどのグラフで $(120,60)$ という点を加えてみると、次のようになります。

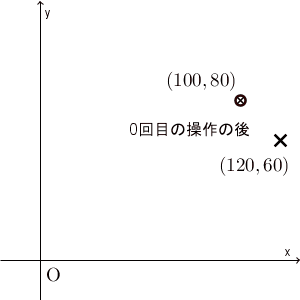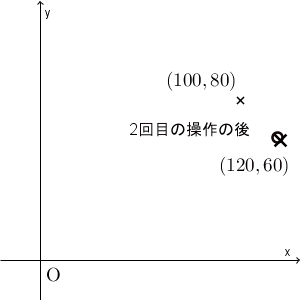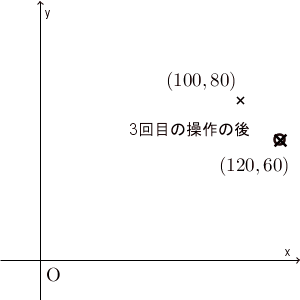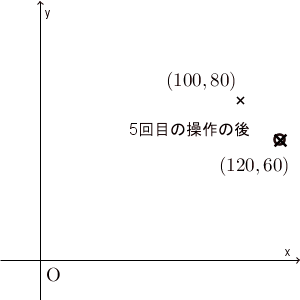
たしかに、 $(x,y)=(100,80)$ から始めると、最終的に $(120,60)$ に近づいて行ってるように見えます。本当に近づいているかどうかを厳密に見るためには、誤差がどうなっているかを見るべきでしょう。次に、誤差について考えてみましょう。

誤差はどう変わっていくか

水の入れ替えによって、 $(x,y)$ だった水の重さは
\begin{eqnarray} \begin{pmatrix} \frac{3}{4} & \frac{1}{2} \\ \frac{1}{4} & \frac{1}{2} \end{pmatrix} \begin{pmatrix} x \\ y \end{pmatrix} &=& \begin{pmatrix} \frac{3}{4}x+\frac{1}{2}y \\ \frac{1}{4}x+\frac{1}{2}y \end{pmatrix} \end{eqnarray}という変換で変わるのでした。 $(x,y)=(100,80)$ として何度も水を入れ替えるとどうなるかは、直接順番に求めていくことは大変だけれども、どうやら $(120,60)$ に近づいていきそうだ、ということがわかったのでした。この状態になれば、何度水を入れ替えても状態が変わらないので、ここで安定するだろう、と考えられるのでしたね。

本当にこの状態に近づくかどうかを確認するために、誤差がどうなるかを考えてみましょう。スタートの状態 $(100,80)$ と、安定すると予想している状態 $(120,60)$ との差は、 $(-20,20)$ となります。

ここで、ちょっと見方を変えて、「コップを分解する」ことを考えてみましょう。つまり、コップ X に入っている水 100 を 120 と -20 に分解する、コップ Y に入っている水 80 を 60 と 20 に分解する、ということです。分解した状態で水を入れ替えて、後で合体させる、と考えます。水が -20 というのは少し考えづらいですが、後で合体させたときにはプラスになるので、今はとりあえず深くは考えずに進みましょう。

$(120,60)$ のペアとなったコップは、水の入れ替えによって何も変わらないのでした。では、 $(-20,20)$ のペアとなったコップはどうでしょうか。変換後の式\[ \frac{3}{4}x+\frac{1}{2}y,\ \frac{1}{4}x+\frac{1}{2}y \]に代入して計算すると、 $(-5,5)$ となることがわかります。両方とも $\dfrac{1}{4}$ 倍になりました。

これは、次のように考えると直感的にわかるでしょう。 X さんに 20万円の借金があり、 Y さんに20万円の貯金があるとします。

水の入れ替えの操作１をこの例で例えるなら、X さんの借金の半分を Y さんに肩代わりしてもらうことに対応します。この結果、Xさんの借金も Yさんの貯金も半分になります。操作２は、さらに Yさんの貯金の半分を X さんに渡すことに対応し、この1セットによって、Xさんの借金も Yさんの貯金も、もとの状態から $\dfrac{1}{4}$ 倍になります。

20万の借金と20万の貯金の場合に限らず、借金と貯金の額が同じなら、同様に $\dfrac{1}{4}$ 倍になります。ただ、同じ額でないときは、計算してみるとわかりますが、こううまくはいきません。

マイナスの水の量ではわかりにくかったかもしれませんが、借金と貯金で考えれば、 $\dfrac{1}{4}$ 倍になることはすんなりわかるでしょう（Yさんの立場だったら、決してわかりたいとは思いませんが）。

さて、これによって何がわかるかをまとめましょう。初期状態の水の重さ $(100,80)$ を、 $(120,60)$ と $(-20,20)$ に分解したのでした。この $(120,60)$ の部分は、何度水の入れ替えを行っても、水の状態は変わらないのでしたね。一方、 $(-20,20)$ は、水の入れ替えを行うごとに、どちらの値も $\dfrac{1}{4}$ 倍ずつされていくのでした。分解したコップを合体すれば元に戻るので、これらのことから、 $n$ 回目の操作の後の状態は、それぞれ、\[ 120-\dfrac{20}{4^n},\ 60+\dfrac{20}{4^n} \]となることがわかります。実際、 $n=1$ とすると、前に求めたように $(115,65)$ となることがわかります。

さらに、何度も繰り返せば $(120,60)$ となることがわかります。 $n$ を大きくしていくと $\dfrac{20}{4^n}$ の部分が $0$ に近づいていくからですね。こうして、 $n$ 回目の操作の後の状態や、最終的にどこに近づいていくかを求めることができました。

初期状態を変えるとどうなるか

$(x,y)=(100,80)$ という初期状態からはじめると、水の入れ替え操作を何度も繰り返していけば $(120,60)$ に近づいていくことがわかりました。では、他の初期状態ではどうなるでしょうか。他の初期状態でも、同じようにある状態に近づくのでしょうか。

少し抽象的にはなりますが、似たような手法で考えることができます。初期状態を $(x,y)$ としましょう。もしこれがある状態に近づいていくなら、水の量は $2:1$ になるはずです。しかも、水の入れ替えで水の合計量は $(x+y)$ のままで変わらないので、それぞれ\[ \frac{2x+2y}{3},\ \frac{x+y}{3} \]となるのではないか、と予想できます。この状態では、何度水の入れ替えを行っても、水の量は変化しません。

では、初期状態からの誤差はどうなるかというと、\[ \frac{x-2y}{3},\ -\frac{x-2y}{3} \]となります（それぞれを足すと、 $x,y$ に戻ります）。よく見ると、符号が違うだけですね。これは、「X さんの借金と Y さんの貯金額が同じ場合」の例を思い出せば、1セットの水の入れ替えによって、どちらももとの量の $\dfrac{1}{4}$ 倍になることがわかります。

以上から、 n 回の操作を行った後の水の量は、 X の方が\[ \frac{2x+2y}{3}+\frac{1}{4^n}\cdot\frac{x-2y}{3} \]となり、Y の方が\[ \frac{x+y}{3}-\frac{1}{4^n}\cdot\frac{x-2y}{3} \]となることがわかります。そして、何度も水の入れ替えを行っていくと、それぞれ\[ \frac{2x+2y}{3},\ \frac{x+y}{3} \]に近づいていくことがわかります。

こうして、どのような初期状態から始めても、水の入れ替えを何度もおこなえば、 $2:1$ の比となるような状態に近づいていくことがわかります。

結局何をやっていたのか

さて、ここまで水の入れ替え問題を見てきました。1セットの操作で水の量がどう変化するかはわかっていましたが、それを使って「何度も入れ替え操作をした場合」を順番に直接計算するのは大変でした。

しかし、水の入れ替えによって不変となる部分（量が $2:1$ となる部分）と、誤差の部分（絶対値が同じで符号が違う部分）とに分解することで、うまい具合に「何度も入れ替え操作をした場合」が計算できるのでした。

これは、今までにあまりない考え方を使っています。操作によって、状態がどう変換されるかがわかっていれば、「n 回の操作をした後はどうなっているか」を考えたい場合、普通は「状態がどう変わっていくか」を計算していくはずです。一方、ここで見たやり方は、変換の方を中心に考えています。変換がきれいに行える都合のいい状態を見つけ出し、それをもとに考えていたわけです。

都合のいい状態とはどういうことか、次の図を見てみましょう。次の図は、青い矢印の先が初期状態の水の量、赤い破線矢印の先が1回の操作をした後の水の量を表しています。初期状態をいろいろ変えて（マイナスになる場合も念のため考えて）、それがどう変換されるかを見ています。

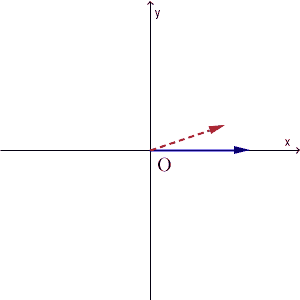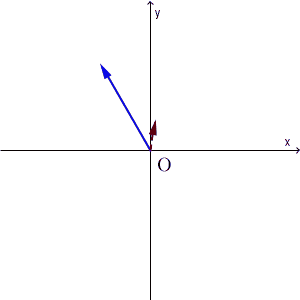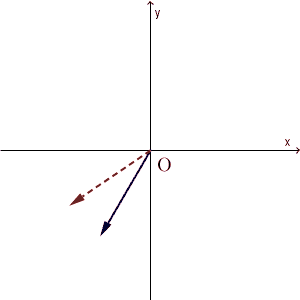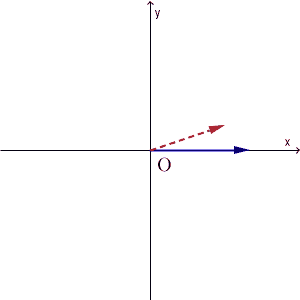
ピッタリ一致するときが2回、長さは違うけど方向が同じときが2回あります。そのときで止めてみると、次のようになります。（反対方向のは無視）

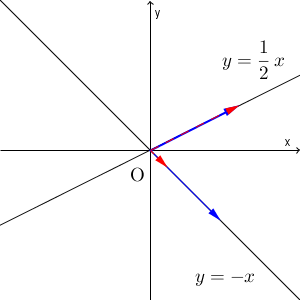
$y=\dfrac{1}{2}x$ を満たしているところでは、変換の前後で向きも大きさも変わりません。 $y=-x$ を満たしているところでは、変換の前後で、大きさは $\dfrac{1}{4}$ 倍になりますが、向きは変わりません。この2つの状態は、今考えている水の入れ替え操作にとって、「向きが変わらない」という点ですごく都合がいいんですね。

そもそも、なぜ「状態がどう変わっていくか」を計算で求めるのが大変だったかというと、
\begin{eqnarray} \begin{pmatrix} \frac{3}{4} & \frac{1}{2} \\ \frac{1}{4} & \frac{1}{2} \end{pmatrix} \begin{pmatrix} x \\ y \end{pmatrix} &=& \begin{pmatrix} \frac{3}{4}x+\frac{1}{2}y \\ \frac{1}{4}x+\frac{1}{2}y \end{pmatrix} \end{eqnarray}という式にもある通り、 $\dfrac{3}{4}$ 倍したものと $\dfrac{1}{2}$ 倍したものを足す、 $\dfrac{1}{4}$ 倍したものと $\dfrac{1}{2}$ 倍したものを足す、というように、掛け算と足し算が毎回混ざって出てくるからなんですね。しかし、 $2x,x$ という初期状態なら \begin{eqnarray} \begin{pmatrix} \frac{3}{4} & \frac{1}{2} \\ \frac{1}{4} & \frac{1}{2} \end{pmatrix} \begin{pmatrix} 2x \\ x \end{pmatrix} &=& \begin{pmatrix} 2x \\ x \end{pmatrix} \end{eqnarray}となり、値は不変です。 $x,-x$ という初期状態なら \begin{eqnarray} \begin{pmatrix} \frac{3}{4} & \frac{1}{2} \\ \frac{1}{4} & \frac{1}{2} \end{pmatrix} \begin{pmatrix} x \\ -x \end{pmatrix} &=& \begin{pmatrix} \frac{1}{4}x \\ -\frac{1}{4}x \end{pmatrix} \end{eqnarray}と $\dfrac{1}{4}$ 倍になります。数を掛けるだけで計算できるようになり、見た目から足し算が消えました。他の状態ではこうはなりません。それは先ほどのグルグル回る図を見ればわかります。この2つの状態以外の場合は、きれいな定数倍の変換にはなりません。

$1$ 倍に変換される部分と $\dfrac{1}{4}$ 倍に変換される部分に分ければ、 $n$ 回変換した後の結果は、（行列ではなく普通の数の） $n$ 乗を使って、簡単に求められるようになります。

変換の推移を見るために、変換の推移を直接計算するのではなく、変換をメインに考えるわけです。変換がきれいに行える「都合のいい状態」を見つける、そして、それらを使って、状態の方を分解する。これは、新しい考え方です。この「都合のいい状態」というのは、一般には固有ベクトルと呼ばれています。行列について学んでいくと、必ず出くわす内容です。

【導入】行列とつるかめ算で見たように、行列は変換を表しています。行列を導入することは、ここで見たような「変換をメインで考える」手法にもつながっていきます。

おわりに

ここでは、（行列で表される）変換を何度も行うとどうなるか、どのような状態に近づいていくかを、水の入れ替え問題を通じて考えていきました。都合のいい状態を見つけ、それを利用すれば、 $n$ 回の入れ替え操作の後の状態を求めることができました。

これは、行列を学んでいくとわかりますが、結果的に、行列の $n$ 乗を計算することに対応しています。そして、ここでは、たまたま固有値や固有ベクトルや逆行列が簡単に見つかったり簡単に計算できる、という状況でしたが、一般的な行列に対して固有ベクトルをどう見つけるか、そしてどうやって $n$ 乗を計算するかなどは、今後行列を学んでいくと見ていくことになるでしょう。