🏠 Home / 数学III / 積分 / 積分と体積

【応用】ドーナツの体積

🕒 2023/07/16

ここでは、積分を使ってドーナツ型の体積を求めます。回転体の体積を求める方法の応用です。

📘 目次

ドーナツの体積

例題

$0\lt r\lt b$ とする。円 $x^2+(y-b)^2=r^2$ を $x$ 軸のまわりに1回転させてできる回転体の体積 $V$ を求めなさい。

円は次のようになっています。

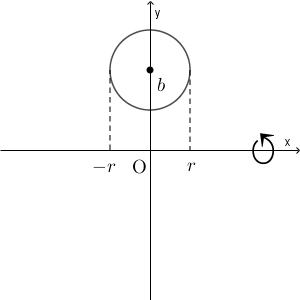
これを $x$ 軸について回転すると、ドーナツ型になります。このドーナツの体積を求める問題です。積分を使えば、このような図形の体積も求められるようになるんですね。

ちなみに、 $0\lt r \lt b$ は、円が $x$ 軸より上にあることを補償するための条件です。

さて、体積を求めるには、断面積を積分すればいいのでした（参考：【基本】積分と回転体の体積）。しかし、今の場合は、真ん中に穴が開いています。どうすればいいでしょうか。

こういう場合は、穴のことを一旦忘れて、後で穴の部分を引けばいいです。

そこで、まずは、以下のような範囲を回転した場合を考えます。

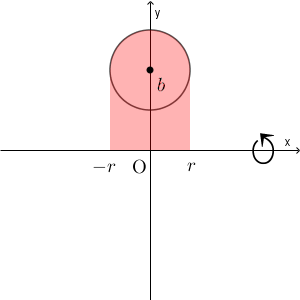
円の上半分、 $x=r$, $x=-r$ で囲まれた部分を $x$ 軸について回転させる、ということです。円の上半分の部分は\[ y=b+\sqrt{r^2-x^2} \]となるので、断面の面積は\[ \pi(b+\sqrt{r^2-x^2})^2 \]と表せることがわかります。

このままでは穴がふさがった状態なので、今度は穴の部分を考えます。次のような範囲を回転させることを考えます。

円の下半分、 $x=r$, $x=-r$ で囲まれた部分を $x$ 軸について回転させる、というわけですね。日常ではドーナツをこのような観点で分けることはないですが、数学で体積を求める場合には、このような「あとで不要な部分を引く」考え方はよく行います。

円の下半分の部分は\[ y=b-\sqrt{r^2-x^2} \]なので、断面の面積は\[ \pi(b-\sqrt{r^2-x^2})^2 \]と表せることがわかります。

あとは積分を計算するだけです。複雑そうですが、いくつかの項が消えるので、それほど大変ではありません。

\begin{eqnarray} & & V \\[5pt] &=& \pi \int_{-r}^r (b+\sqrt{r^2-x^2})^2 dx \\[5pt] & & -\pi \int_{-r}^r (b-\sqrt{r^2-x^2})^2 dx \\[5pt] &=& \pi \int_{-r}^r 4b\sqrt{r^2-x^2} dx \\[5pt] &=& 4\pi b \int_{-r}^r \sqrt{r^2-x^2} dx \\[5pt] \end{eqnarray}ここで、最後の式の積分は、置換積分をしてもいいのですが、よく考えると、半径 $r$ の円の半分の面積を表している（参考：【標準】楕円で囲まれた部分の面積と積分）ので $\dfrac{\pi r^2}{2}$ だとわかります。こうして \begin{eqnarray} V &=& 4\pi b\cdot\frac{\pi r^2}{2} \\[5pt] &=& 2 \pi^2 b r^2 \end{eqnarray}となります。これが答えとなります。

ちなみに、この体積 $V$ は次のように変形することができます。\[ V=\pi r^2 \cdot 2\pi b \]前半の $\pi r^2$ とは、もとの円の面積ですね。後半の $2\pi b$ は、円の中心 $(0,b)$ が描く軌跡（円周）の長さに一致します。