【基本】積分と回転体の体積

🕒 2023/07/15 🔄 2023/07/16

ここでは、積分を使って回転体の体積を求める方法を見ていきます。球の体積がなぜあの式で求められるかもわかります。

📘 目次

回転体の体積

【基本】積分を使って体積を求めるで見たように、断面を積分することで立体の体積を求めることができます。これの特別版である、回転体の体積について考えます。

$y=f(x)$ を考えます。簡単のため、つねに $0$ 以上の値をとるとします。これと、 $x=a$, $x=b$, $x$ 軸で囲まれた部分について考えます（$a\lt b$ とします）。

この部分を $x$ 軸について回転してできる回転体の体積 $V$ を考えましょう。

これを、平面 $x=c$ で切ると、断面は円です。半径は $f(c)$ なので、断面積は $\pi \{f(c)\}^2$ となります。よって、これを積分すれば体積がわかるわけですね。\[ V=\pi \int_a^b \{f(x)\}^2 dx \]と求めることができます。

回転体の体積

$y=f(x)$ がつねに $0$ 以上の値をとるとする。 $y=f(x)$ と $x=a$, $x=b$, $x$ 軸で囲まれた部分を、 $x$ 軸について回転させてできる回転体の体積は、以下のようにして求められる。\[ V=\pi \int_a^b \{f(x)\}^2 dx \]

球の体積

先ほど見た内容の例として、球の体積について考えてみます。

円の方程式 $x^2+y^2=r^2$ について考えます。これを $x$ 軸について回転して球を作りたいのですが、上半分を回転すると円の下半分も通過することがわかります。そこで、この上半分のみについて考えます。 $x$ 軸について回転すると、半径 $r$ の球ができあがります。

$-r\leqq c\leqq r $ として、この球を、平面 $x=c$ で切ることを考えます。この断面の面積を求めましょう。

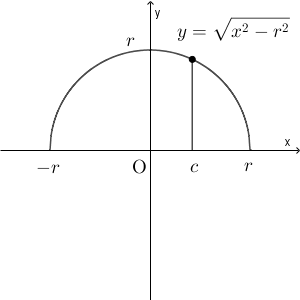
円の方程式を変形すれば、 $y=\sqrt{r^2-x^2}$ となります。このことから、平面 $x=c$ で切ったとき、断面の円周上の点は、 $x$ 軸と $\sqrt{r^2-c^2}$ だけ離れていることがわかります。つまり、断面の半径は $\sqrt{r^2-c^2}$ ということです。

これより、断面の面積がわかるので、積分をすれば体積が求められます。以下のようになります。
\begin{eqnarray} & & \int_{-r}^r \pi (\sqrt{r^2-x^2})^2 dx \\[5pt] &=& \pi \int_{-r}^r (r^2-x^2) dx \\[5pt] &=& 2\pi \int_0^r (r^2-x^2) dx \\[5pt] &=& 2\pi \left[r^2x -\frac{1}{3}x^3\right]_0^r \\[5pt] &=& 2\pi \left(r^3 -\frac{1}{3}r^3\right) \\[5pt] &=& \frac{4}{3}\pi r^3 \end{eqnarray}たしかに、今までに学んだ球の体積と一致していますね。積分を学べば、昔は謎だった体積の公式を証明することができるようになります。

球の場合、円を回転させる場合と、上半分の半円を回転させる場合とでは、同じ結果になります。勘のいい人は予想できるかもしれませんが、 $x$ 軸の上側と下側で形が違っていた場合は、回転したときに自分自身と重なってしまう可能性があります。この場合は、自分と交わってしまう部分を考慮して計算しなくてはならず、考えるのも計算するのも面倒になります。

このような問題は大学入試でも出題されます。別のページで取り上げることにしましょう。