【応用】連立一次不等式（変な解）

【標準】連立一次不等式で連立一次不等式の解き方を見ましたが、この記事では解が少し変わったものになる例を挙げていきたいと思います。解き方は同じですが、共通範囲を考えるときに変わったことが起きる例です。

変な連立一次不等式その１

まずは次の例題を解いてみましょう。

まず、それぞれの不等式を解きます。1つ目の不等式は次のようになります。
\begin{eqnarray} 3(2x-1) & \gt & 4x-5 \\ 6x-3 & \gt & 4x-5 \\ 2x & \gt & -2 \\ x & \gt & -1 \\ \end{eqnarray}続いて、2つ目の不等式は次のように解けます。 \begin{eqnarray} x-5 & \leqq & 5(x-1) \\ x-5 & \leqq & 5x-5 \\ -4x & \leqq & 0 \\ x & \geqq & 0 \\ \end{eqnarray} この2つの共通範囲が解なので、数直線を使って共通範囲がどうなるか考えてみます。

この図を見てわかる通り、$x\geqq 0$ は $x\gt -1$ に含まれます。なので、この共通部分というのは、$x\geqq 0$ となります。これが答えです。共通部分と言うと交わっているような印象を受けますが、片方が片方を完全に包んでいる場合もあるんですね。

ちなみにこれは何が起こっているかというと、この例題で言えば、「2つ目の不等式を満たしたときは、必ず1つ目の不等式も満たす」ということです。2つ条件があるけれど、実質的には1つの条件しか効いていない、ということですね。

変な連立一次不等式その２

変わった例第2弾です。

先ほどの例題とほぼ同じです。違うのは、1つ目の不等号の向きだけです。なので、先ほど解いた途中の結果を使えば、1つ目の不等式の解は $x\lt -1$ であり、2つ目の不等式の解は、$x\geqq 0$ となります。

よって、数直線を使うと、範囲は次のようになります。

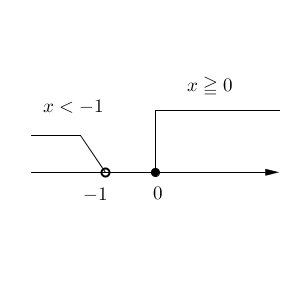
「共通部分」がないんですね。ということで、この不等式の解はありません。「解なし」が答えです。

「共通部分がない」という場合もあり得るんですね。

変な連立一次不等式その３

さて、最後の例題です。これもまた変わった例です。

これも2つ目の不等式は先ほどと同じです。1つ目の不等式だけが違います。1つ目の不等式を解くと、次のようになります。
\begin{eqnarray} 3(2x-1) & \leqq & 4x-3 \\ 6x-3 & \leqq & 4x-3 \\ 2x & \leqq & 0 \\ x & \leqq & 0 \\ \end{eqnarray}2つ目の不等式の解は、前の例題で解いた通り、$x\geqq 0$ です。これら2つの共通範囲を考えましょう。

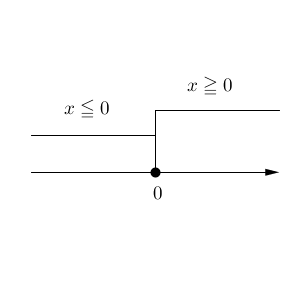
少し図が分かりにくいですね。段差をつけているのは、右側が0以上で左側が0以下を表していることをわかりやすくするためです。例題2のように共通部分がないようにも見えますが、実は $x=0$ が両方の範囲に入っているんですね。つまり、 $x=0$ がこの連立一次不等式の解になります。

不等式の解が、範囲ではないこともあるんですね。

ちなみに、もし「$x\geqq 0$ と $x\lt 0$」だったら、共通範囲はありません。前者に0は入りますが、後者には入りません。そのため、もし2つの不等式を解いて「$x\geqq 0$ と $x\lt 0$」となれば、「解なし」が答えになります。

おわりに

ここでは、少し変わった解になる連立不等式の例を見てきました。片方が片方に含まれてしまう場合、共通部分がない場合、共通部分が1点しかない場合、がありました。どんな例であっても、数直線で考えれば間違いは減ります。計算を確かめるためにも、数直線をかいて考える癖をつけておきましょう。