🏠 Home / 数学C / 平面上の曲線 / 二次曲線

【応用】放物線となる軌跡

🕒 2018/04/21 🔄 2023/05/01

ここでは、軌跡が放物線となるような問題を考えます。

📘 目次

放物線となる軌跡

例題

円 $(x-3)^2+y^2=4$ に外接し、直線 $x=-1$ に接する円の中心 P の軌跡を求めなさい。

点 P の座標を $(x,y)$ として、 $x,y$ が満たすべき条件を考えていきましょう。点 P を中心とする円を、円 P とします。

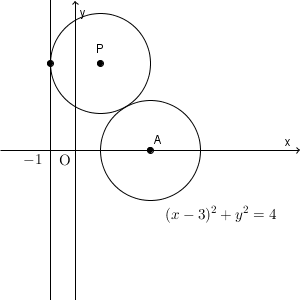
図から、条件を満たすとき、 $x\gt -1$ であることがわかります。

「円 P が、直線 $x=-1$ に接する」という条件を考えましょう。このことから、円 P の半径は $x+1$ となることがわかります。 $x\gt -1$ なので、 $x+1$ は正で、絶対値はつけなくても大丈夫です。

次に、「円 P がもう一つの円に外接する」という条件を考えます。 $(x-3)^2+y^2=4$ は、中心 $(3,0)$ で半径が $2$ の円です。この中心を A とすると、\[ \mathrm{ AP }=\sqrt{(x-3)^2+y^2} \]となります。よって、円 P の半径は、これから $2$ を引いた値とかくこともできます。

以上から
\begin{eqnarray} \sqrt{(x-3)^2+y^2}-2 &=& x+1 \\[5pt] \sqrt{(x-3)^2+y^2} &=& x+3 \\[5pt] x^2-6x+9+y^2 &=& x^2+6x+9 \\[5pt] y^2 &=& 12x \\[5pt] \end{eqnarray}となります。

逆に、 $y^2=12x$ を満たすとき、 $x\gt -1$ の条件下では、式変形を逆にたどっていくことで条件を満たしていることがわかります。よって、放物線 $y^2=12x$ が求める軌跡であることがわかります。

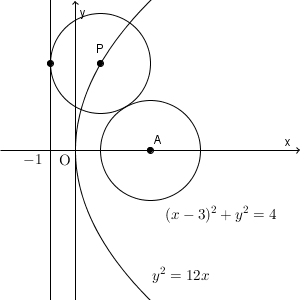
このように、計算によって軌跡を求めることもできますが、もう少し図形的な性質を用いて考えることもできます。

上では、点 P が直線 $x=-1$ に接し、円 $(x-3)^2+y^2=4$ にも接するということから、円 P の半径を考えました。ここで、 AP の長さについて考えてみましょう。この長さは、円 P の半径に $2$ を加えたものになります。なので、この長さは、点 P と直線 $x=-3$ との距離に等しいことがわかります。