【応用】三角形の傍心

🕒 2022/09/03 🔄 2023/05/03

ここでは、三角形の傍接円や傍心について見ていきます。外心、内心、重心と比べると、登場頻度はかなり低いですが、内容自体はそれほど難しくはありません。

📘 目次

傍心の存在

【基本】三角形の内心で見たように、三角形の内心とは、3つの内角の二等分線が交わる点のことをいうのでした。下の図でいえば、点 $\mathrm{I}$ のことです。

この内心を中心とし、3つの辺に接する円がかけます。この円を内接円というのでしたね。

ここで、内角の二等分線ではなく、外角の二等分線を考えてみます。上の図の三角形 $\mathrm{ABC}$ について、 $\angle \mathrm{B}$, $\angle \mathrm{C}$ の外角の二等分線をかきます。この交点を $\mathrm{J}$ としましょう。

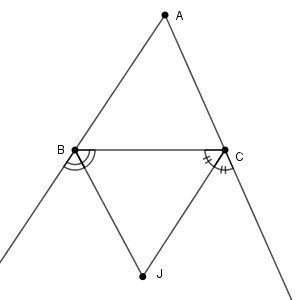
このとき、 $\mathrm{J}$ から直線 $\mathrm{BC,CA,AB}$ に下した垂線の足を $\mathrm{D,E,F}$ とします。

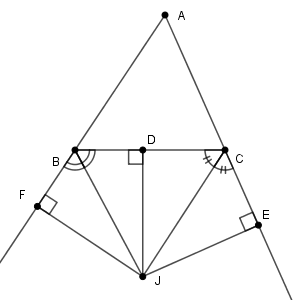
角の二等分線の性質から、 $\mathrm{JF=JD}$ と $\mathrm{JE=JD}$ が成り立つことがわかります。なので、 $\mathrm{JF=JE}$ が言えるので、 $\mathrm{J}$ が $\angle \mathrm{A}$ の二等分線上にあることがわかります。

このように、 $\triangle \mathrm{ABC}$ に対し、 $\angle \mathrm{A}$ の二等分線と $\mathrm{B, C}$ における外角の二等分線は、1点に交わります。この点を $\angle \mathrm{A}$ に対する傍心(ぼうしん、excenter) といいます。

$\mathrm{JD=JE=JF}$ なので、傍心を中心にして、3つの辺の延長線に接する円をかくことができます。これを傍接円といいます。

同じようにして、$\angle \mathrm{B}$ に対する傍心、$\angle \mathrm{C}$ に対する傍心も存在することが示せます。つまり、三角形に対して、傍心は3点あります。

三角形の五心

三角形には、5種類の特徴的な点があることがわかりました。

外心: 各辺の垂直二等分線が交わる点（3頂点からの距離が等しい点）
内心: 3つの内角の二等分線が交わる点（3辺からの距離が等しい点）
重心: 3つの中線が交わる点
垂心: 各頂点から対辺に下した垂線が交わる点
傍心: 1つの内角の二等分線と残りの角の外角の二等分線が交わる点（それぞれの内角に対して1点ある）

この5種類の点を合わせて、三角形の五心（ごしん）と呼びます。数学の世界ではこう呼ぶのですが、高校数学ではあまり傍心が出てこないので、この「五心」という言葉もあまり出てきません。

傍心と内心の関係

傍心も内心も、角の二等分線が絡んでいます（内角か外角か、の違いはあります）。そのため、内接円も傍接円も辺を含む直線に接する、という点は同じです。内接円は3つの辺と接し、傍接円は延長線上で接する点が異なります。

他にも、点の作り方から、いい性質がわかります。

次の画像のように、 $\triangle \mathrm{ABC}$ の3つの傍心を、それぞれ、 $\mathrm{J,K,L}$ としましょう。また、内心を $\mathrm{I}$ とします。

このとき、 $\angle \mathrm{IBJ}$ を考えてみます。 $\mathrm{BI}$ が $\angle \mathrm{B}$ の二等分線、 $\mathrm{BJ}$ が $\angle \mathrm{B}$ の外角の二等分線でした。なので、 $\angle \mathrm{IBJ}$ は、 $\angle \mathrm{B}$ の内角の半分と外角の半分を足したものです。つまり、 $90^{\circ}$ というわけです。

他も同様にすると、 $\mathrm{AJ\perp KL}$, $\mathrm{BK\perp LJ}$, $\mathrm{CL\perp JK}$ となることがわかります。つまり、三角形 $\mathrm{ABC}$ の内心 $\mathrm{I}$ は、3つの傍心を頂点にした三角形 $\mathrm{JKL}$ の垂心と一致していることがわかります。