【応用】三次不等式が常に成り立つ条件
ここでは、与えられた三次不等式が常に成り立つ条件を求める問題を考えます。
三次不等式が常に成り立つ条件
三次不等式については、【標準】三次不等式の証明でも見ました。問題文にあるような「 $0$ より大きい」という不等式は、「(考えている範囲での)最小値が $0$ より大きい」というふうに考えればいいのでしたね。そうすると、【基本】微分と最大値・最小値で見たように、微分をして最小値を求める問題に帰着されます。
ということで、まずは微分をして最小値を求める、という方針で考えていきましょう。
$f(x)=x^3-3ax^2+16a$ とすると
\begin{eqnarray}
f'(x)
&=&
3x^2-6ax \\[5pt]
&=&
3x(x-2a) \\[5pt]
\end{eqnarray}となります。
この計算から、 $f'(x)=0$ ならば $x=0,2a$ ということがわかります。次に増減表をかいていくことになるのですが、少し問題があります。 $0$ と $2a$ はどちらが大きいのか決まっていません。どちらが大きいかによって、増減表自体が変わってきます。そのため、増減表が変わるポイントで場合分けをする必要があります。
今、考える範囲は $x\geqq 0$ の部分だけです。 $2a \lt 0$ であれば、考えている範囲に $x=2a$ は含まれず、増減表は次のようになります。
\begin{array}{c|ccccc}
x & 0 & \cdots \\
\hline
f’(x) & & + \\
\hline
f(x) & f(0) & \nearrow
\end{array}$x\geqq 0$ の範囲では単調増加となり、最小値は $f(0)=16a$ となります。しかし、この最小値が $0$ より大きくなることはありません( $a\lt 0$ という条件下で考えているからです)。よって、この場合は、つねに不等式が成り立つ、ということは起こりません。
また、 $2a=0$ のときも、増減表は先ほどと同様になり、この場合も $x\geqq 0$ の範囲では単調増加となります。先ほどと同じ理由で、この場合もつねに不等式が成り立つ、ということはありません。
最後に、 $2a \gt 0$ の場合を考えましょう。この場合は、考えている範囲( $x\geqq 0$ )に、 $2a$ が含まれるため、次のような増減表になります。
\begin{array}{c|ccccc}
x & 0 & \cdots & 2a & \cdots \\
\hline
f’(x) & & - & 0 & + \\
\hline
f(x) & f(0) & \searrow & f(2a) & \nearrow
\end{array}増減表より、この場合は、最小値が $f(2a)$ となります。
さて、この最小値 $f(2a)$ が正となれば、与えられた不等式が常に成り立つ、ということが言えます。 $f(2a)\gt 0$ となる a の範囲を求めてみましょう。
\begin{eqnarray}
f(2a) & \gt & 0 \\[5pt]
(2a)^3-3a(2a)^2+16a & \gt & 0 \\[5pt]
-4a^3+16a & \gt & 0 \\[5pt]
a^3-4a & \lt & 0 \\[5pt]
a(a-2)(a+2) & \lt & 0 \\[5pt]
\end{eqnarray}左辺が正になるところを求めるため、簡易的にグラフをかくと次のようになります。
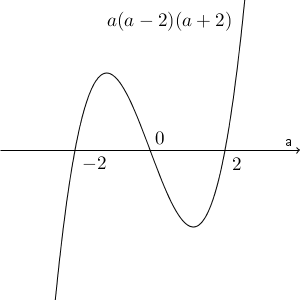
符号がわかればいいので、左辺を微分して丁寧にグラフをかく必要は特にありません。このグラフを見れば、左辺が正になるのは\[ a\lt -2, \ 0\lt a \lt 2 \]のとき、となります。今考えている範囲は $2a \gt 0$ だったので、\[ 0\lt a \lt 2 \]だけが該当することがわかります。
以上より、3つのケースから\[ 0\lt a \lt 2 \]が求める答えであることがわかります。このとき、左辺の最小値は正となり、つねに不等式が成り立ちます。
おわりに
ここでは、三次不等式が常に成り立つ条件を求める問題を考えました。
「常に不等式が成り立つ」を「最大・最小となる場合でも不等式が成り立つ」と言い換えて考えるようにしましょう。微分をすれば、最大・最小を求めることができるようになります。ただし、係数や範囲に文字が入っている場合は、状況によって、最大・最小をとる場所が異なることがあります(参考:【応用】三次関数の最大・最小(極値が動く) や 【応用】三次関数の最大・最小(区間が動く))。その場合は、場合分けをして考えるようにします。
することが多いですが、今まで見てきたことを組み合わせて考えていきましょう。





