【応用】空間における2直線のなす角

🕒 2023/09/24 🔄 2023/09/25

ここでは、空間での2直線のなす角を定義するときに、なぜ好きな位置に動かしてもいいのかを見ていきます。

📘 目次

【基本】空間における2直線の位置関係で、空間における2直線のなす角についてみました。ねじれの位置にあるときには、2直線が交わるように平行移動して、そのときの角を使うのでした。

ただ、厳密にいうと、このように定めることにした場合、移動する位置によって角の大きさが変わらないのか、確かめる必要があります（高校の教科書ではたいてい省略していますが）。以下では、このことを証明していきます。

2直線のなす角が定義できることについて

空間上の2直線 $m,n$ について考えていきます。

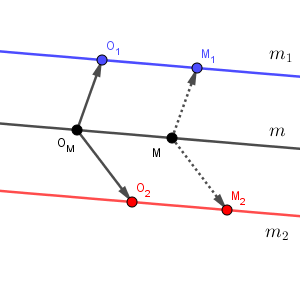
空間上に2点 $\mathrm{O_1}, \mathrm{O_2}$ をとったとします。直線 $m$ 上に2点 $\mathrm{O_M,M}$ をとり、点 $\mathrm{O_M}$ が $\mathrm{O_1}$ と一致するように直線 $m$ を平行移動します。このとき、直線 $m$ は直線 $m_1$ に、点 $\mathrm{M}$ は点 $\mathrm{M_1}$ に移動するとします。同様に、点 $\mathrm{O_M}$ が $\mathrm{O_2}$ と一致するように直線 $m$ を平行移動したとき、直線 $m$ は直線 $m_2$ に、点 $\mathrm{M}$ は点 $\mathrm{M_2}$ に移動するとしましょう。

同様に、 $n$ 上に $\mathrm{O_N,N}$ をとって、点 $\mathrm{O_N}$ が $\mathrm{O_1,O_2}$ と一致するように直線 $n$ を平行移動したとき、直線 $n$ はそれぞれ直線 $n_1,n_2$ に、点 $\mathrm{N}$ はそれぞれ点 $\mathrm{N_1,N_2}$ に移動するとします。

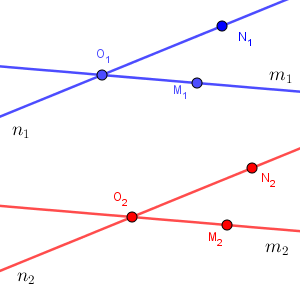
$\mathrm{O_1,O_2}$ は適当にとった点なので、もしも $\angle \mathrm{M_1 O_1 N_1}=\angle \mathrm{M_2 O_2 N_2}$ がいえれば、点のとり方によらず、2直線のなす角が一定だといえます。なので、空間上の2直線のなす角を定められるといえます。

それでは、 $\angle \mathrm{M_1 O_1 N_1}=\angle \mathrm{M_2 O_2 N_2}$ を示していきます。

平行移動をして点を決めたので、 $\mathrm{O_1M_1}=\mathrm{O_2M_2}$ がいえます。また、「平行かつ平行なら平行」なので、 $\mathrm{O_1M_1}/\!/\mathrm{O_2M_2}$ もいえます（参考：【応用】空間における平行な3直線）。

よって、四角形 $\angle \mathrm{O_1 M_1 M_2 O_2}$ は平行四辺形です（1組の辺が等しくて平行）。なので、 $\mathrm{O_1O_2}=\mathrm{M_1M_2}$ と $\mathrm{O_1O_2} /\!/ \mathrm{M_1M_2}$ がいえます。同様にして、 $\mathrm{O_1O_2}=\mathrm{N_1N_2}$ と $\mathrm{O_1O_2} /\!/ \mathrm{N_1N_2}$ もいえます。

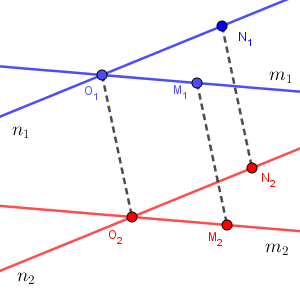
これより、$\mathrm{M_1M_2}=\mathrm{N_1N_2}$ と $\mathrm{M_1M_2} /\!/ \mathrm{N_1N_2}$ がわかるので、四角形 $\mathrm{M_1 N_1 N_2 M_2}$ も平行四辺形だといえます。

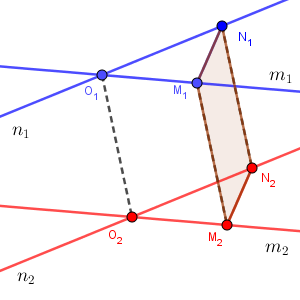
だから、 $\mathrm{M_1N_1}=\mathrm{M_2N_2}$ がいえます。よって、3組の辺がそれぞれ等しいから、 $\triangle\mathrm{O_1M_1N_1}\equiv\triangle\mathrm{O_2M_2N_2}$ なので、示したかった、 $\angle \mathrm{M_1 O_1 N_1}=\angle \mathrm{M_2 O_2 N_2}$ がいえます。

どこに平行移動してもなす角は変わらないことがわかったので、2直線が交わるように好きな場所に平行移動してからなす角を考えればいいことがわかります。