🏠 Home / 数学A / 図形の性質 / 空間における直線と平面

【応用】空間における平行な3直線

🕒 2023/09/23 🔄 2023/09/26

ここでは、空間における直線について、「平行かつ平行なら平行」であることを示していきます。

📘 目次

平行かつ平行なら平行

ここでは、次のことを示します。

平行な3つの直線

空間における3直線 $\ell,m,n$ について、 $\ell /\! / m$ かつ $m /\! / n$ とする。このとき、 $\ell /\! / n$ が成り立つ。

成り立つのが自然に思えるかもしれませんが、これも示すことができます。

直線 $\ell,m,n$ が同一平面上にある場合は明らかに成り立つので、以下では、この3直線は同一平面上にないとします。

直線 $m$ 上に、点 $\mathrm{M}$ をとります。この点 $\mathrm{M}$ から、直線 $\ell,n$ に垂線を下ろし、その足をそれぞれ $\mathrm{L,N}$ とおきます。

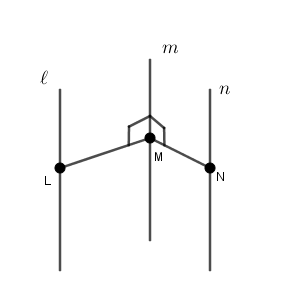
ここで、【応用】平面に垂直な直線でみた、「直線が平面に垂直であることを示すには、その平面上の2本の直線と垂直であることを示せばいい」という内容を使いましょう。そうすると、直線 $m$ は、平面 $\mathrm{LMN}$ 上にある2直線 $\mathrm{LM}, \mathrm{MN}$ と垂直なので、直線 $m$ は平面 $\mathrm{LMN}$ と垂直であることがわかります。

また、【応用】平面に垂直な2直線でみた、「2本の直線が平行で片方が平面に垂直なら、もう片方の直線もその平面に垂直」という内容を使います。すると、$m /\!/ \ell$ より、直線 $\ell$ も平面 $\mathrm{LMN}$ と垂直で、同様に、直線 $n$ も平面 $\mathrm{LMN}$ と垂直である、といえます。

さらに、【応用】平面に垂直な2直線でみた、「2直線がある平面に垂直なら、その2直線は平行」という内容を使ってみます。

そうすると、直線 $\ell,n$ がどちらも平面 $\mathrm{LMN}$ に垂直であることから、$\ell /\!/ n$ となることがいえます。

これで証明終わりです。

過去に示したことを使って、「平行かつ平行なら平行」を示すことができました。