【応用】平面に垂直な2直線

🕒 2023/09/23 🔄 2023/09/26

ここでは、空間において、平面に垂直な2直線に関する性質を見ていきます。文章で書くと、「2本の直線が平行で片方が平面に垂直なら、もう片方の直線もその平面に垂直」「2直線がある平面に垂直なら、その2直線は平行」です。

📘 目次

平行な2直線と平面に垂直な直線

ここでは、次のことを示します。

平行な2直線と平面に垂直な直線

2直線 $\ell,m$ が平行で、 $\ell$ が平面 $\alpha$ に垂直なら、 $m$ も平面 $\alpha$ に垂直である。

なお、これを示すために、【応用】平面に垂直な直線でみた、「直線が平面に垂直であることを示すには、その平面上の2本の直線と垂直であることを示せばいい」という内容を使います。厳密には、同じ点で平面と直線が交わる場合しか示していませんが、以下の証明ではそのケースしか出てきません。

さて、示していきます。

$\ell,m$ が平行なので、この2直線を含む平面が存在します。その平面を、 $\beta$ と呼ぶことにしましょう。

$\ell$ と平面 $\alpha$ は共有点を持つので、平面 $\alpha$ と $\beta$ は交わります。この交線と $\ell,m$ との交点を $\mathrm{A,C}$ とおきます。また、 $\ell,m$ 上に、 $\mathrm{A,C}$ とは異なる点 $\mathrm{B,D}$ をとります。

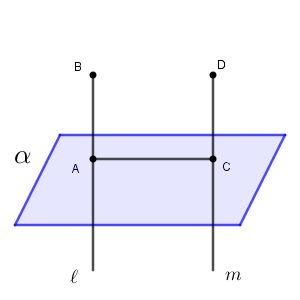
$\ell \perp \alpha$ なので、 $\mathrm{AB\perp AC}$ です。また、 $\mathrm{AB /\!/ CD}$ で錯角は等しいから、$\mathrm{CD\perp AC}$ となります。（なので、 $\mathrm{CD}$ が平面 $\alpha$ 上の他の直線と垂直であることが示せれば、上で紹介した内容から、 $\mathrm{CD}\perp\alpha$ がいえることになります）

平面 $\alpha$ 上で、点 $\mathrm{C}$ を通り、直線 $\mathrm{AC}$ に垂直な直線を引き、この直線上で $\mathrm{AB=CE}$ を満たす点 $\mathrm{E}$ をとります。

このとき、 $\triangle \mathrm{ABC} \equiv \triangle \mathrm{CEA}$ （2組の辺とその間の角がそれぞれ等しい）なので、$\mathrm{BC=AE}$ が成り立ちます。これより、 $\triangle \mathrm{ABE} \equiv \triangle \mathrm{CEB}$ （3組の辺がそれぞれ等しい）なので、 $\angle\mathrm{BAE}=\angle\mathrm{ECB}$ がいえます。ここで、 $\ell\perp\alpha$ より、 $\mathrm{AB\perp AE}$ だから、 $\angle \mathrm{ECB}=90^{\circ}$ がいえます。

これから、 $\mathrm{CE\perp AC}$ と $\mathrm{CE\perp BC}$ より、 $\mathrm{CE}\perp\beta$ がいえます（$\beta$ は $\mathrm{A,B,C,D}$ を含む平面と定義していました）。このことから、 $\mathrm{CD\perp CE}$ がいえます。これと $\mathrm{CD\perp AC}$ より、 $\mathrm{CD}\perp\alpha$ となります。

こうして、 $m\perp\alpha$ が示せました。

平面に垂直な2直線

つづいて、平面に垂直な2直線に関する次の内容をみていきます。

平面に垂直な2直線

2直線 $\ell,m$ がどちらも平面 $\alpha$ に垂直なら、 $\ell /\!/ m$ である。

$\ell,m$ と平面 $\alpha$ との交点を $\mathrm{A,C}$ とおきます。また、 $\ell,m$ 上に、 $\mathrm{A,C}$ とは異なる点 $\mathrm{B,D}$ をとります。

さっきと図が一緒ですね。しかし、条件が違っている点に注意しましょう。今回は、2直線が平面に垂直だとわかっていますが、2直線が平行かどうかがわかっていません。

まず、 $\ell\perp\alpha,m\perp\alpha$ より、$\mathrm{AB\perp AC}, \mathrm{CD\perp AC}$ が成り立ちます。

「このことから $\mathrm{AB /\!/ CD}$ が言えるのでは？」と思うかもしれませんが、これだけでは正しくありません。【基本】空間における2直線の位置関係で見たように、空間の場合、「垂直かつ垂直なら平行」は一般には成り立ちません。

方針としては、4点 $\mathrm{A,B,C,D}$ が同一平面上にあることを示していきます。3点 $\mathrm{A,C,D}$ から決まる平面を $\beta$ として、 $\mathrm{B}$ が平面 $\beta$ 上にあることを示します。4点が同じ平面上にあれば、錯角が等しいことより平行であることが示せます。

さて、平面 $\alpha$ 上で、点 $\mathrm{C}$ を通り、直線 $\mathrm{AC}$ に垂直な直線を引き、この直線上で $\mathrm{AB=CE}$ を満たす点 $\mathrm{E}$ をとります。 $\ell\perp\alpha,m\perp\alpha$ より、$\mathrm{AB\perp AE}, \mathrm{CD\perp CE}$ が成り立ちます。

また同じ図が出てきましたね。 $\mathrm{CE\perp CA}$ と $\mathrm{CE\perp CD}$ なので、3点 $\mathrm{A,C,D}$ から決まる平面 $\beta$ と $\mathrm{CE}$ とは垂直です。よって、 $\mathrm{B}$ が平面 $\beta$ 上にあることをいうには、 $\mathrm{CE\perp CB}$ が言えればいいです。

$\triangle \mathrm{ABC} \equiv \triangle \mathrm{CEA}$ （2組の辺とその間の角がそれぞれ等しい）なので、$\mathrm{BC=AE}$ が成り立ちます。これより、 $\triangle \mathrm{ABE} \equiv \triangle \mathrm{CEB}$ （3組の辺がそれぞれ等しい）なので、 $\angle\mathrm{BAE}=\angle\mathrm{ECB}$ がいえます。ここで、 $\ell\perp\alpha$ より $\angle \mathrm{BAE}=90^{\circ}$ だから、 $\angle \mathrm{ECB}=90^{\circ}$ がいえます。

こうして、 $\mathrm{CE\perp CB}$ が言えるので、点 $\mathrm{B}$ は、 $\mathrm{C}$ を通る $\mathrm{CE}$ に垂直な平面 $\beta$ 上にあることがわかります。4点 $\mathrm{A,B,C,D}$ が同一平面上にあることが言えました。このことと、錯角が等しいことから $\ell /\!/ m$ がわかります。これで証明終わりです。