【競プロ】和の公式（1からnまでの和）

🕒 2019/11/22 🔄 2023/05/01

ここでは、 $1$ から $n$ までの和を求める公式を見ていきます。for文を使って繰り返し足しても求められますが、もっと簡単に求める方法があります。組合せを利用して考えていきます。競プロ記事の一覧はこちら。

📘 目次

総当たり戦の総数

次の問題文を見てみましょう：AtCoder ABC 139 E - League。 $N$ 人のテニスの選手が総当たり戦をします。このとき、合計で $\dfrac{N(N-1)}{2}$ 試合が行われる、と問題文には書かれています。この式はどこから来たのでしょう。

$N$ 人を円形に並べて、試合を線で表すことにしましょう。線の数が試合の数に対応しています。下の図は、 $N=5$ のときです。

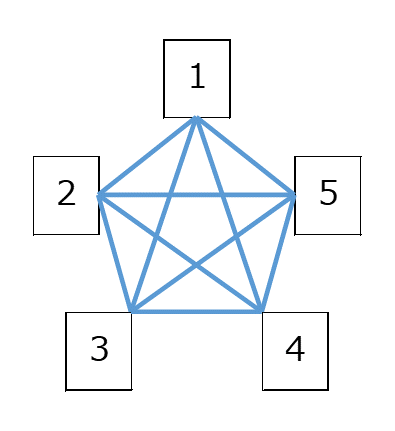
総当たり戦というのは、それぞれの選手が、自分以外の人全員と試合をする、ということです。そのため、ある選手に着目すると、その選手は $N-1$ 回試合をすることになります。

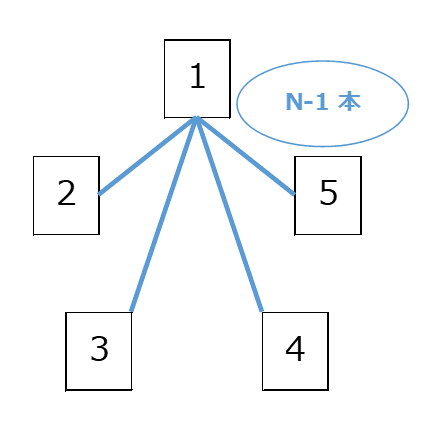
これを全選手に対して同じように考えると、 $N$ 倍すればいいように感じられます。しかし、 A 選手からみた B 選手との試合と B 選手から見た A 選手との試合は、同じ内容なのに、1つの試合を2回ずつ数えてしまっていることがわかります。

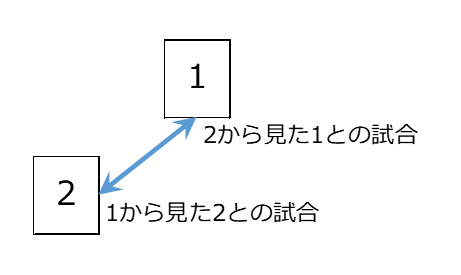
このことから、試合の総数は\[ (N-1)\times N \div 2 = \dfrac{N(N-1)}{2} \]と計算できることがわかります。

別の考え方として、試合をする2人の選手を選ぶ、という方法もあります。 $N$ 人の選手から2人を選べば、試合が1つ決まります。選手の選び方と試合は1つ1つ対応するので、選び方の総数が試合総数と一致します。つまり、 ${}_N\mathrm{C}_2$ が試合数であり、これは $\dfrac{N(N-1)}{2}$ と表すことができます。

これらから、 $N$ 人の選手が総当たり戦をするときの試合数は $\dfrac{N(N-1)}{2}$ となることがわかります。

自然数の和

先ほどの総当たり戦の総数を、別の観点で考えてみます。ダブらせずに試合数を数えることを考えます。

選手に $1$ から $N$ までの番号をつけることにしましょう。選手 $1$ の人は、自分以外の全員と試合をするので、選手 $1$ が出る試合は $N-1$ 試合あります。

次に、選手 $2$ を考えます。今回はダブらせずに数えるようにします。選手 $1$ との試合はすでに数えたので、選手 $2$ が出る試合でまだ数えていないものは、選手 $3$ から選手 $N$ までの $N-2$ 人との試合です。

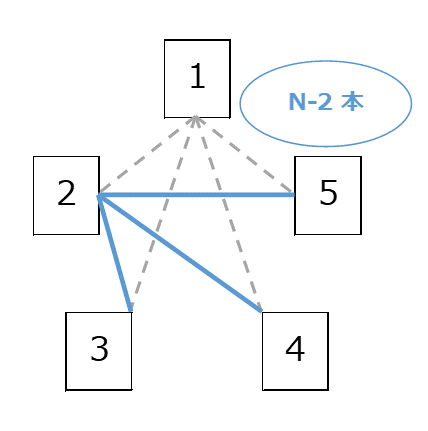
なので、ダブらせないように数えると、選手 $2$ が出る試合は $N-2$ 試合あります。

同様に、すでに数えている試合を除いてダブらないように数えると、選手 $3$ が出る試合は $N-4$ 試合、選手 $4$ が出るものは $N-5$ 試合、…、となっていきます。選手 $N-1$ が出るものは、選手 $N$ との試合だけだから $1$ 試合。選手 $N$ が出る試合は、すでに全部数えているので $0$ です。

以上から、すべての試合数は、$(N-1)+(N-2)+\cdots+3+2+1$ という式で書けます。 $1$ から $N-1$ までの和です。先ほど試合数は $\dfrac{N(N-1)}{2}$ とも求めていたので、この両者は等しくなります。つまり、次の式が成り立ちます。\[ 1+2+3+\cdots +(N-2)+(N-1)=\dfrac{N(N-1)}{2} \]また、実際には、 $N-1$ までの和より、 $N$ までの和を求めることが多いので、上の式で $N-1$ を $N$ に置き換えた式が公式としてよく使われます。右辺は $\dfrac{(N+1)(N+1-1)}{2}=\dfrac{(N+1)N}{2}$ なので、次のように書くことができます。\[ 1+2+3+\cdots +(N-1)+N=\dfrac{N(N+1)}{2} \]この式は、数学でも競プロでも、いろいろなところで登場します。

1 から N までの和

$1$ から自然数 $N$ までの自然数の和は、 $\dfrac{N(N + 1)}{2}$ で表すことができる。

$1$ から $N$ までの和を求めるには、【競プロ】和や階乗と再帰関数で見たように、再帰関数を使う方法もありますし、for文を使う方法もありますが、どちらにしても $N$ 回程度の計算が必要です。しかし、 $\dfrac{N(N+1)}{2}$ の公式を使えば、1回の計算で答えが出せます。そのため、普通はこちらの式を使います。

この内容を踏まえると、AtCoder ABC 043 A - キャンディーとN人の子供イージーが解けます。また、上のリンクでも紹介しましたが、AtCoder ABC 099 B - Stone Monumentなども解けるでしょう。