【基本】書き出して数える

🕒 2017/01/06 🔄 2023/05/01

ここでは、数え方の基本である「すべてを書き出して数える」方法を見ていきます。

📘 目次

経路の数を数える

下のような図を使って、経路の数を数える問題を考えてみましょう。

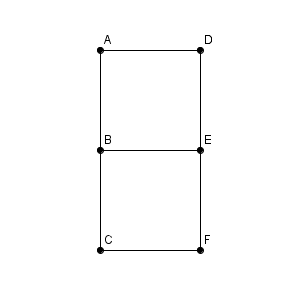
この図で、Ｂを出発し、すべての道を1回ずつ通ってＥに行く経路は何通りあるでしょうか。

いろいろ試してみると、Ｅに行く方法は何通りかあることがわかります。しかし、すべての経路の数を数えるには、思いつくままに挙げていくのはよくありません。モレやダブりが発生するかもしれないからです。

こういう場合は、書き出してみましょう。そのときに重要なのは、モレなくダブりなく数えるということです。整理して数えていきます。実際にやってみましょう。

Ｂを出発した後は、上に行くか右に行くか下に行くか、この3パターンがあります。この3つに分けてそれぞれ考えて行きます。

まずは、上に行くパターンを考えてみます。Ｂ⇒Ａと進むと、後はＤ⇒Ｅと進んで行くことになります。Ｅに到着した後は、左に行くか下に行くか、2パターンあります。左に行った場合は、Ｂ⇒Ｃ⇒Ｆ⇒Ｅとなり、下に行った場合は、Ｆ⇒Ｃ⇒Ｂ⇒Ｅとなります。つまり、このときは2通りであることがわかります。

次に、Ｂを出発して右に行くパターンを考えましょう。Ｅについた後、上に行くか下に行くか、2パターンあります。そしてその後は、一本道です。なので、このときも2通りであることがわかります。

最後に、下に行くパターンですが、これは「上に行くパターン」と同じように考えれば2パターンになることがわかります。Ｂ⇒Ｃ⇒Ｆ⇒Ｅと行き、その後は、左に行くか上に行くかの2パターン。それぞれその後は一本道なので、2パターンとなるわけですね。

結局、次の6通りであることがわかりました。

思いつくままに経路を挙げていくと、モレが出てしまうかもしれません。しかし、「一番初めにどっちに移動するか」で場合分けをすれば、モレもダブりもありません。その後も、経路が分かれるたびに経路数を数え、すべてを足し合わせれば全体の経路数になります。

場合の数を数えるときは、「すべてのケースを書き出す」というのが基本です。

ここでは、場合の数を数えるために、「すべてを書き出して数える」方法を見てきました。この方法は確実であり、原理的には「間違うことはない」と言えます。

しかし、書き出すのは面倒です。例えば、「5人が1列に並ぶ方法は何通りあるか」を書き出して解くのは大変です。120通りもあるからです。テストなら、書き出すだけで時間切れになってしまいます。

「書き出して数える」のは数え方の基本ですが、ほとんどの問題ではもっと簡単に計算だけで解くことができます。その方法は、場合の数の分野で学んでいくことになります。

対象者：数学A

トピック：数え方の基本

レベル：基本

キーワード：場合の数経路

チャンネル登録はコチラから（以下は、動画のサンプルです）