【基本】ベクトルの成分と座標
ここでは、ベクトルの成分と座標について見ていきます。見た目が同じなのでまぎらわしいですが、ベクトルなのか座標なのか、注意してみていきましょう。
原点と点を結んだベクトル
原点 $\mathrm{O}(0,0)$ と点 $\mathrm{A}(a_1,a_2)$ を結んだベクトル $\overrightarrow{ \mathrm{ OA } }$ を考えましょう。
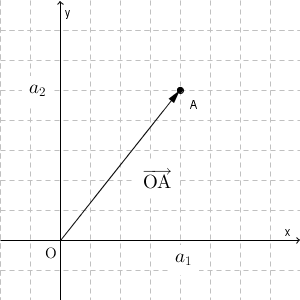
このとき、 $\overrightarrow{ \mathrm{ OA } }$ の成分を考えてみましょう。といっても、 x 成分が $a_1$ で、 y 成分が $a_2$ であることがすぐにわかるので、次のような成分表示になります。\[ \overrightarrow{ \mathrm{ OA } }=(a_1,a_2) \]
紛らわしいですが、 $\mathrm{A}(a_1,a_2)$ と書けば、座標のことです。 $\overrightarrow{ \mathrm{ OA } }=(a_1,a_2)$ と書けば、ベクトルの成分表示です。見た目は同じですが、意味は違います。注意しましょう。
点と点を結んだベクトル
点 $\mathrm{A}(a_1,a_2)$ と点 $\mathrm{B}(b_1,b_2)$ を結んでできるベクトル $\overrightarrow{ \mathrm{ AB } }$ を考えましょう。
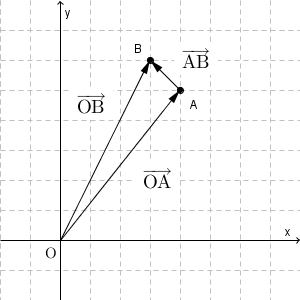
先ほど見たことから、\[ \overrightarrow{ \mathrm{ OA } }=(a_1,a_2),\ \overrightarrow{ \mathrm{ OB } }=(b_1,b_2) \]と書けることがわかります。また、【標準】平行四辺形とベクトルの演算で見たように、ベクトルを次のように分解してみましょう。\[ \overrightarrow{ \mathrm{ AB } }=\overrightarrow{ \mathrm{ AO } }+\overrightarrow{ \mathrm{ OB } }=-\overrightarrow{ \mathrm{ OA } }+\overrightarrow{ \mathrm{ OB } } \]
これらの変形から、 $\overrightarrow{ \mathrm{ AB } }$ を成分で書くと、
\begin{eqnarray}
\overrightarrow{ \mathrm{ AB } }
&=&
\overrightarrow{ \mathrm{ OB } }-\overrightarrow{ \mathrm{ OA } } \\[5pt]
&=&
(b_1,b_2)-(a_1,a_2) \\[5pt]
&=&
(b_1-a_1,b_2-a_2) \\[5pt]
\end{eqnarray}となります。
順番に気をつけましょう。 $\overrightarrow{ \mathrm{ AB } }$ の成分は、 B の座標から A の座標を引いて求めます。 $\overrightarrow{ \mathrm{ AB } }$ が、点 A から見た点 B の位置だ、と考えれば、理解しやすいでしょう。
具体的な例で計算すると、 $\mathrm{ A }(4,5)$, $\mathrm{ B }(3,6)$ のとき、 $\overrightarrow{ \mathrm{ AB } }$ を成分で表すと
\begin{eqnarray}
\overrightarrow{ \mathrm{ AB } }=(3,6)-(4,5)=(-1,1)
\end{eqnarray}となります。
おわりに
ここでは、点の座標がわかっているときに、それらを使ってできるベクトルの成分について見てきました。座標は原点を基準としているので、原点を基準にしたベクトル(上の例でいう $\overrightarrow{ \mathrm{ OA } }$ や $\overrightarrow{ \mathrm{ OB } }$ )を使って考えることができます。表現方法が紛らわしいので注意しましょう。





