【基本】鈍角の三角比

🕒 2016/09/28 🔄 2023/05/01

ここでは、鈍角に対して三角比を定義する方法を見ていきます。直角三角形を使った定義では鋭角に対してしか定義できないので、違う手法を考えます。

📘 目次

動機

【基本】三角比の定義（直角三角形による定義）で見た通り、三角比は、角度と直角三角形、直角三角形と辺の比、という流れで定義しました。しかし、【標準】２つの直角三角形に分解して三角比を求めるで見た通り、直角三角形でなくても、三角比を考えることができます。なので、これから、直角三角形以外の三角形に対しても、三角比を考えていきたいんですね。

ただ、そこでネックになることがあります。というのも、鈍角（90度より大きい角）の三角比をどうやって決めるかを考えないといけません。鋭角の三角比なら、直角三角形を考えて辺の比を考えればよかったんですが、鈍角だと直角三角形を作ることができません。なので、何か一工夫が必要となってきます。

鈍角の三角比の定義

鈍角に対しても三角比が定義できるようにするには、結論から書くと、直角三角形ではなくて円を使います。

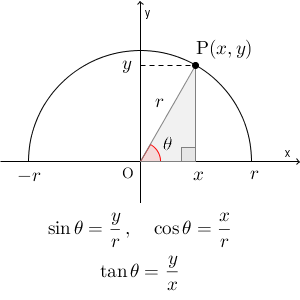
この図は、半径 r の半円（上半分）です。点 O は原点、点 A は $(r,0)$ とします。点 P はこの半円上の点で、 $(x,y)$ とします。ここで、 $\angle \mathrm{ POA }=\theta$ とすると、鋭角のときには次のような関係式が成り立ちます。\[ \sin\theta = \frac{y}{r},\ \cos\theta = \frac{x}{r},\ \tan\theta = \frac{y}{x} \]ここまでは、鋭角の三角比の定義と整合性がとれています。

そして、鈍角の三角比は、これを使って定義するんですね。 $\theta$ を大きくしていけば、点 P は円の左側にいきます。このときの P の座標を使って、\[ \sin\theta = \frac{y}{r},\ \cos\theta = \frac{x}{r},\ \tan\theta = \frac{y}{x} \]と定義します。

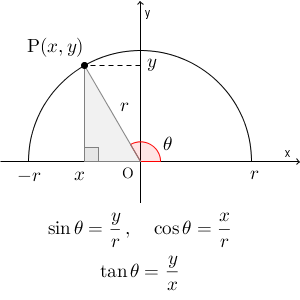
鋭角のときのような直角三角形を持ち出して定義することはできません。そのかわりに、鋭角のときに成り立っていたものを、鈍角の場合でも成り立つように定義した、というわけです。

数学では、このように、「ある領域で成り立っていたものを、整合性がとれたまま、さらに広い領域で成り立つように定義する」ということをよくします。これを「拡張する」といいます。上の話は、三角比を拡張したことになります。

具体的な値

例えば、 $\sin 120^{\circ}$, $\cos 120^{\circ}$, $\tan 120^{\circ}$ を考えてみます。次のように、半径 $2$ の半円で考えてみます。

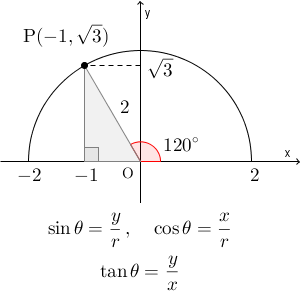
この図から、定義通りに計算すると\[ \sin 120^{\circ}=\frac{\sqrt{3} }{2},\ \cos 120^{\circ}=-\frac{1}{2},\ \tan 120^{\circ}=-\sqrt{3} \]となります。

この結果からもわかる通り、三角比が負になることもあるんですね。鈍角の場合、上の定義にある点 P は第2象限にあるので、 x 座標が負になります。なので、この場合は $\cos$ と $\tan$ は負になります。

上の定義を使うと、 $0^{\circ}$ や $180^{\circ}$ の三角比を考えることもできます。図をかいて考えると、次のようになることが分かります。
\begin{eqnarray} \sin 0^{\circ}&=&0 \\ \cos 0^{\circ}&=&1 \\ \tan 0^{\circ}&=&0 \\[5pt] \sin 180^{\circ}&=&0 \\ \cos 180^{\circ}&=&-1 \\ \tan 180^{\circ}&=&0 \\ \end{eqnarray}

$90^{\circ}$ の場合は、次のようになります。
\begin{eqnarray} \sin 90^{\circ} = 1 \\ \cos 90^{\circ} = 0 \end{eqnarray} なお、 $\tan\theta = \dfrac{y}{x}$ の式からもわかる通り、 $\theta=90^{\circ}$ のときは分母が $0$ になってしまうため、 $\tan\theta$ は定義できません。