【基本】三角比の相互関係（鈍角）

【基本】三角比の相互関係では、 $\sin$, $\cos$, $\tan$ の間に成り立つ関係式を見ました。そのとき、角度は鋭角に限っていたのですが、その関係式は鈍角でも成り立ちます。ここでは、そのことを見ていきましょう。

三角比の相互関係

半径1の円（単位円）を考えます。 $\mathrm{ O }(0,0)$, $\mathrm{ A }(1,0)$ とし、半円（上半分）の円周上に、 $\angle \mathrm{ POA }=\theta$ となる点 P をとります。

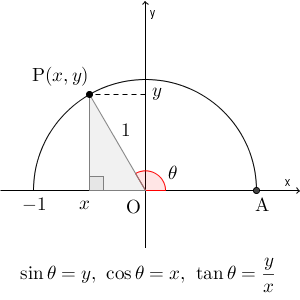
このとき、 $\mathrm{ P }(x,y)$ とすると、 $\cos\theta=x$, $\sin\theta=y$, $\displaystyle \tan\theta=\frac{y}{x}$ となるのでしたね。

さて、ここで、鋭角のときに、 $\sin$, $\cos$, $\tan$ の間に次のような関係があったことを思い出しましょう。（参考：【基本】三角比の相互関係）

• $\displaystyle \tan\theta = \frac{\sin\theta}{\cos\theta}$
• $\sin^2\theta +\cos^2\theta = 1$
• $\displaystyle \tan^2\theta +1 = \frac{1}{\cos^2\theta}$

これらの関係式は、鈍角の場合ではどうなるでしょうか。

1つ目の式は、両辺とも $\displaystyle \frac{y}{x}$ になるので、成り立つことが分かります。

2つ目の式の左辺は、 $x^2+y^2$ であり、三平方の定理からこれは半径の2乗になります。なので、右辺と一致します。

3つ目の式は、2つ目の式の両辺を $\cos^2\theta$ で割り、1つ目の式を適用すれば得られます。

ということで、角度が鈍角になっても、同じようにこの関係式は成り立ちます。

例題

三角比の相互関係を使った例題を解いてみましょう。

(1)を見てまず注意することは、 $\tan\theta$ が負、ということです。このことから、 $\theta$ は鈍角であることがわかります。このことは後で使うので、覚えておきましょう。

相互関係の3つ目の式を使うと、次のように計算できます。
\begin{eqnarray} (-2)^2 +1 &=& \frac{1}{\cos^2\theta} \\ \cos^2\theta &=& \frac{1}{5} \\ \end{eqnarray}ここで、 $\theta$ が鈍角であることから、 $\cos\theta$ が負であることが分かります。よって、 $\displaystyle \cos\theta=-\frac{\sqrt{5} }{5}$ となります。

相互関係の1つ目の式から、 $\sin\theta$ は次のように計算できます。
\begin{eqnarray} \sin\theta &=& \tan\theta\cos\theta \\ &=& -2\times\left(-\frac{\sqrt{5} }{5}\right) \\ &=& \frac{2\sqrt{5} }{5} \\ \end{eqnarray}

次に、(2)ですが、相互関係の2つ目の式を使って、 $\cos$ を求めます。
\begin{eqnarray} \cos^2\theta = 1-\sin^2\theta=\frac{8}{9} \end{eqnarray}$\cos$ はマイナスの値もとる可能性があるため、 $\displaystyle \cos\theta=\pm\frac{2\sqrt{2} }{3}$ となります。どちらも答えになります。【基本】三角方程式のときにも見たように、 $\sin\theta=\bigcirc$ となる $\theta$ は、2つ存在することがあるんですね。

$\tan\theta$ は、 $\cos\theta$ の値に応じて、場合分けをして考えないといけません。相互関係の1つ目の式から $\displaystyle \tan\theta = \frac{\sin\theta}{\cos\theta}$ なので、 $\displaystyle \cos\theta = \frac{2\sqrt{2} }{3}$ のときは $\displaystyle \tan\theta = \frac{\sqrt{2} }{4}$ となり、 $\displaystyle \cos\theta = -\frac{2\sqrt{2} }{3}$ のときは $\displaystyle \tan\theta = -\frac{\sqrt{2} }{4}$ となります。

よって、答えは、\[ \left(\cos\theta,\tan\theta\right)=\left(\frac{2\sqrt{2} }{3},\frac{\sqrt{2} }{4}\right),\left(-\frac{2\sqrt{2} }{3},-\frac{\sqrt{2} }{4}\right) \]となります。2組とも答えになるので、どちらも答えないといけません。なお、前者は $\theta$ が鋭角、後者は鈍角の場合になっています。

ちなみに、上では $\tan\theta$ を求めるときに、 $\tan\theta=\dfrac{\sin\theta}{\cos\theta}$ という関係式を用いましたが、相互関係には $\tan^2\theta+1=\dfrac{1}{\cos^2\theta}$ という関係式もありましたね。こちらを使うとどうなるでしょう。

この式に代入すると、 $\tan^2\theta=\dfrac{1}{8}$ となり、$\tan\theta=\pm\dfrac{\sqrt{2}}{4}$ となります。このままだと、符号が特定できません。つまり、このように計算してしまうと、 $\cos\theta$ が正で $\tan\theta$ が負の場合なども含まれてしまいます。角度が鋭角でも鈍角でも、こんなことは起こりません。

三角比の相互関係には、2乗を使ったものがありますが、これを使うと符号の特定ができなくなる可能性があります。できる限り $\tan\theta=\dfrac{\sin\theta}{\cos\theta}$ を優先的に使うようにしましょう。

おわりに

ここでは、三角比の相互関係が鈍角の場合でも成り立つことを見ました。また、この関係を使って、ある三角比の値がわかった場合に、別の三角比を求める問題も考えました。鈍角の場合が入ってくると、符号がマイナスになることもあるので、注意して考えるようにしましょう。