【基本】三角比と2直線のなす角
円を使った三角比の定義では、 $\tan$ は「角度→直線の傾き」という対応で考えましたが、ここでは、「直線の傾き→角度」という流れで考える問題を見ていきます。
例題
$\tan$ を定義したときに、角度から直線の傾きを考えました。今の問題では、これを逆に使って、直線の傾きから角度を考えてみましょう。
図をかくと、次のような状況になっています。
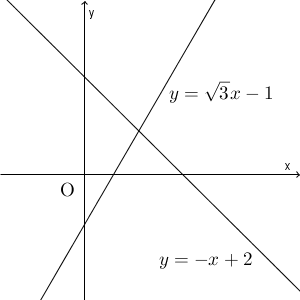
ただ、この図を眺めていても、少しわかりづらいですね。 $\tan$ を定義したときは、原点を中心とする円をかいて考えたので、この問題でも直線を平行移動して原点を通るようにしてみましょう。平行移動しても、2直線のなす角は変化しません。
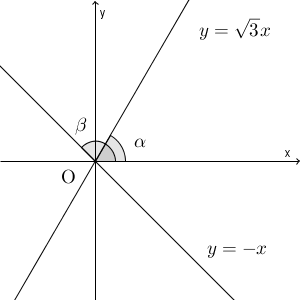
つまり、2つの直線 $y=-x$ と $y=\sqrt{3}x$ のなす角を求めればいいんですね。 x 軸の $x\geqq 0$ の部分と、それぞれの直線の $y\geqq 0$ の部分とのなす角を、それぞれ $\alpha$, $\beta$ とします(0度以上180度以下とします)。このとき、 $\tan$ は直線の傾きになるので
\begin{eqnarray}
\tan \alpha &=& \sqrt{3} \\
\alpha &=& 60^{\circ} \\
\end{eqnarray}とわかり、
\begin{eqnarray}
\tan \beta &=& -1 \\
\beta &=& 135^{\circ} \\
\end{eqnarray}もわかります。
よって、 $\theta = 135^{\circ} -60^{\circ} =75^{\circ}$ と求めることができます。
おわりに
ここでは、直線の傾きから角度を考える問題を見ました。 $\tan$ に関連付けて考えれば解くことができます。また、直線 $x=1$ を引いて直角三角形を作って解くこともできますね。三角比や直角三角形を通じ、角度と直線の傾きとを対応させて考えましょう。





