【基本】よく出る0度から180度までの三角比の値

🕒 2016/09/29 🔄 2023/05/01

ここでは、0度から180度までの中で、よく登場する角度の三角比をまとめておきます。慣れないうちは、この記事にあるような図をかいて考えましょう。

📘 目次

この記事の内容は以下の動画でも解説しています。

0度から90度まで

直角三角形を使った定義ではなく、円を使った定義で90度までの三角比を考えます。鋭角の場合は、直角三角形で考えたときと、値は同じです。

円を使った三角比の定義では、半径 r の円を考え、 $\mathrm{ A }(r,0)$ として、 $\angle \mathrm{ POA }=\theta$ となる点 $\mathrm{ P }(x,y)$ をとって、\[ \sin\theta=\frac{y}{r}, \ \cos\theta=\frac{x}{r},\ \tan\theta=\frac{y}{x} \]とするのでしたね。

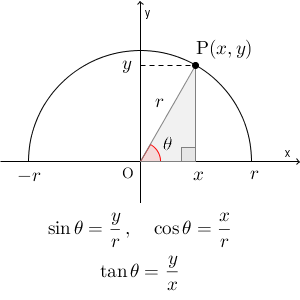
最終的に比を考えることになるので、はじめから半径は $1$ としておいたほうが、何かと便利になります。

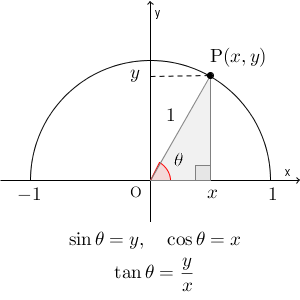
そうすると、さきほどの式は次のようにもっと簡潔に書けます。\[ \sin\theta=y,\ \cos\theta=x,\ \tan\theta=\frac{y}{x} \]x 座標が $\cos\theta$ 、 y 座標が $\sin\theta$ 、OP の傾きが $\tan\theta$ になる、ということですね。

これを踏まえて、点の座標から、よく出る三角比の値をおさえておきましょう。

この図から、0度から90度まででよく出る角度の三角比は、次のようになります。（ $\tan 90^{\circ}$ は定義できません）

$\theta$	$0^{\circ}$	$30^{\circ}$	$45^{\circ}$	$60^{\circ}$	$90^{\circ}$
$\sin\theta$	$0$	$\dfrac{1}{2}$	$\dfrac{\sqrt{2} }{2}$	$\dfrac{\sqrt{3} }{2}$	$1$
$\cos\theta$	$1$	$\dfrac{\sqrt{3} }{2}$	$\dfrac{\sqrt{2} }{2}$	$\dfrac{1}{2}$	$0$
$\tan\theta$	$0$	$\dfrac{\sqrt{3} }{3}$	$1$	$\sqrt{3}$	×

90度から180度まで

同様に、90度から180度も図をかいて考えます。

90度から180度で、よく出る角度の三角比をまとめておきます。

$\theta$	$90^{\circ}$	$120^{\circ}$	$135^{\circ}$	$150^{\circ}$	$180^{\circ}$
$\sin\theta$	$1$	$\dfrac{\sqrt{3} }{2}$	$\dfrac{\sqrt{2} }{2}$	$\dfrac{1}{2}$	$0$
$\cos\theta$	$0$	$-\dfrac{1}{2}$	$-\dfrac{\sqrt{2} }{2}$	$-\dfrac{\sqrt{3} }{2}$	$-1$
$\tan\theta$	×	$-\sqrt{3}$	$-1$	$-\dfrac{\sqrt{3} }{3}$	$0$

分母を２にすると見えてくるもの

ここまでに紹介したもののうち、 $\sin\theta$, $\cos\theta$ について、規則性が見えやすい表し方があるので、紹介します。

$0=\sqrt{0}$, $1=\sqrt{1}$, $2=\sqrt{4}$ であることを利用すれば、次のように書くことができます。

$\theta$	$0^{\circ}$	$30^{\circ}$	$45^{\circ}$	$60^{\circ}$	$90^{\circ}$	$120^{\circ}$	$135^{\circ}$	$150^{\circ}$	$180^{\circ}$
$\sin\theta$	$\dfrac{\sqrt{0} }{2}$	$\dfrac{\sqrt{1} }{2}$	$\dfrac{\sqrt{2} }{2}$	$\dfrac{\sqrt{3} }{2}$	$\dfrac{\sqrt{4} }{2}$	$\dfrac{\sqrt{3} }{2}$	$\dfrac{\sqrt{2} }{2}$	$\dfrac{\sqrt{1} }{2}$	$\dfrac{\sqrt{0} }{2}$
$\cos\theta$	$\dfrac{\sqrt{4} }{2}$	$\dfrac{\sqrt{3} }{2}$	$\dfrac{\sqrt{2} }{2}$	$\dfrac{\sqrt{1} }{2}$	$\dfrac{\sqrt{0} }{2}$	$-\dfrac{\sqrt{1} }{2}$	$-\dfrac{\sqrt{2} }{2}$	$-\dfrac{\sqrt{3} }{2}$	$-\dfrac{\sqrt{4} }{2}$

$\dfrac{\sqrt{\Box} }{2}$ の形でそろえると、$\sqrt{\Box}$ の部分は、 $\sin\theta$ なら $\sqrt{0}$ → $\sqrt{4}$ → $\sqrt{0}$ と変化し、 $\cos\theta$ なら $\sqrt{4}$ → $\sqrt{0}$ → $-\sqrt{4}$ と変化することがわかります。わかりやすい変化になっていますね。

三角比のとる値の特徴

今度は、辺の比がわかりやすい角度以外についても見ていきます。

$0^{\circ} \leqq \theta \leqq 180^{\circ}$ の範囲で、三角比のとる値の特徴を見てみます。そして、最後に表でまとめます。

$\sin\theta$ は y 座標を、 $\cos\theta$ は x 座標を表していたので、次のことが図からわかります。\[ 0\leqq \sin\theta \leqq 1, \ -1\leqq\cos\theta\leqq 1 \]また、角度 $\theta$ を $0^{\circ}$ から徐々に大きくしていくと、 $\sin\theta$ は $90^{\circ}$ になるまで徐々に大きくなり、 $90^{\circ}$ 以降は、徐々に小さくなっていきます。一方、 $\cos\theta$ は、角度が大きくなれば点は左に移動していくので、角度が大きくなるほど値が小さくなっていくことがわかります。

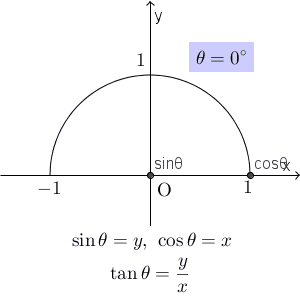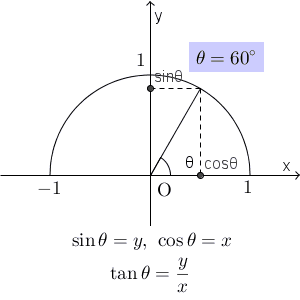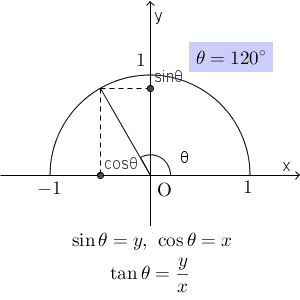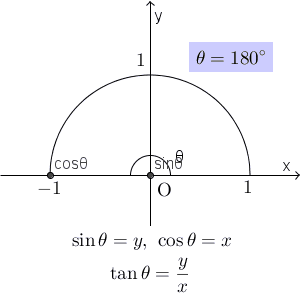
$\tan\theta$ は直線の傾きを表していました。角度が大きくなっていくと、傾きは急になっていくので、 $90^{\circ}$ までは値がどんどん大きくなり、すべての正の実数値をとります。また、 $90^{\circ}$ を超えると、直線は右肩下がりで、徐々に緩やかになっていくので、値はマイナスの値から0に近づいていきます。これも、 $90^{\circ}$ に近づけていくとわかる通り、すべての負の実数値をとります。

これらのことをまとめて、表にします。

$\theta$	$0^{\circ}$	$\cdots$	$90^{\circ}$	$\cdots$	$180^{\circ}$
$\sin\theta$	$0$	小 ⇒ 大（正の値）	$1$	大 ⇒ 小（正の値）	$0$
$\cos\theta$	$1$	大 ⇒ 小（正の値）	$0$	大 ⇒ 小（負の値）	$-1$
$\tan$	$0$	小 ⇒ 大（正の値）	×	小 ⇒ 大（負の値）	$0$