【基本】三角方程式

🕒 2016/10/01 🔄 2023/05/01

今までは、角度から三角比を求めていましたが、ここでは三角比から角度を考えてみます。といっても、角度が求まるような三角比は種類が限られているので、慣れてくれば結果は自然と覚えられるかもしれません。

📘 目次

cosの場合

三角比から角度を求めてみましょう。まずは、 $\cos$ の例です。

$0^{\circ}\leqq \theta \leqq 180^{\circ}$ とします。このとき、半径1の円（単位円）を使った定義では、 $\sin$, $\cos$, $\tan$ が、それぞれ y 座標、 x 座標、傾き、を表すんでしたね。

では、まず、次の値を満たす $\theta$ を考えてみましょう。\[ \cos\theta = -\frac{1}{2} \]これを考えるには、まずは単位円をかいて、直線 $\displaystyle x=-\frac{1}{2}$ との交点を考えます。この交点が、求める $\theta$ に対応しています。

直線 $x=-\dfrac{1}{2}$ と単位点との交点を P 、x 軸との交点を H とすると、この図から、三角形 OPH が、 $\mathrm{ OH }:\mathrm{ OP }:\mathrm{ PH }=1:2:\sqrt{3}$ の三角形になることがわかります。よって、 $\angle \mathrm{ POH }=60^{\circ}$ なので、 $\theta=120^{\circ}$ と求められます。

慣れるまでは、このような単位円をかいて考えましょう。

sinの場合

続いては、 $\sin$ の値から角度を求めてみます。 $0^{\circ}\leqq \theta \leqq 180^{\circ}$ として、次を満たす $\theta$ を考えてみます。\[ \sin\theta = \frac{\sqrt{2} }{2} \]これも、単位円をかいて考えましょう。今回は $\sin$ なので、直線 $\displaystyle y=\frac{\sqrt{2} }{2}$ もかきます。

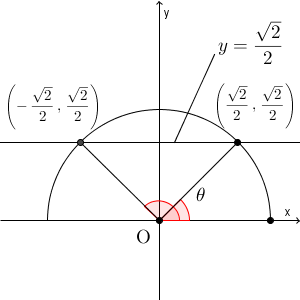
すると、交点は図のように2つできます。どちらも、 x 軸へ垂線を下すと、 $1:1:\sqrt{2}$ の三角形ができるので、 $\theta=45^{\circ},135^{\circ}$ の2つが答えとなります。両方とも答えないと、正解にはなりません。

tanの場合

最後に、 $\tan$ の値から角度を求めてみます。 $0^{\circ}\leqq \theta \leqq 180^{\circ}$ として、次を満たす $\theta$ を考えてみます。\[ \tan\theta = -\frac{\sqrt{3} }{3} \]今回は、傾きなので、単位円と直線 $x=1$ をかいて考えます。