【基本】三角形の内心

ここでは、三角形の内接円や内心について見ていきます。

角の二等分線

三角形の内心の話をする前に、角の二等分線についておさらいをしておきましょう。

$\angle \mathrm{AOB}$ に対し、 $\angle \mathrm{POA}=\angle \mathrm{POB}$ となる点 $\mathrm{P}$ をとります。

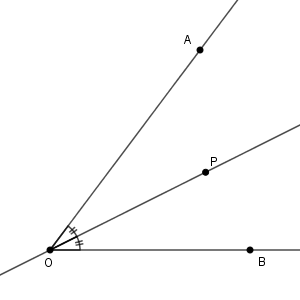
このとき、直線 $\mathrm{OP}$ のことを $\angle \mathrm{AOB}$ の二等分線といいます。

以下では、点 $\mathrm{P}$ は角の内部にあるとします。

点 $\mathrm{P}$ から直線 $\mathrm{OA, OB}$ に垂線をおろし、その足をそれぞれ $\mathrm{X, Y}$ とします。

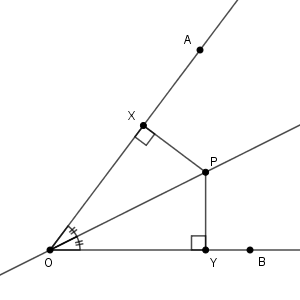
このとき、$\mathrm{OP}$ が共通、 $\angle \mathrm{XOP}=\angle \mathrm{YOP}$、 $\angle \mathrm{PXO}=\angle \mathrm{PYO}=90^{\circ}$ なので、 $\triangle \mathrm{POX}$ と $\triangle \mathrm{POY}$ は合同です（直角三角形で、斜辺と1つの鋭角がそれぞれ等しいため）。なので、 $\mathrm{PX=PY}$ が成り立ちます。言い換えると、二等分線上の点は直線 $\mathrm{OA,OB}$ から等距離にある、ということです。

逆に、 $\mathrm{P'}$ から $\mathrm{OA, OB}$ に下した垂線の足を $\mathrm{X',Y'}$ としたときに、 $\mathrm{P'X'=P'Y'}$ を満たすとしましょう。（点 $\mathrm{P'}$ も角の内部にあるとします）

このとき、$\triangle \mathrm{P'OX'}$ と $\triangle \mathrm{P'OY'}$ が合同であることがいえます（直角三角形で、斜辺と他の1辺がそれぞれ等しいため）。よって、 $\angle \mathrm{P'OA}=\angle \mathrm{P'OB}$ がいえるので、 $\mathrm{P'}$ は $\angle \mathrm{AOB}$ の二等分線上にあることがわかります。

以上から、次のことがいえます。

このことを使って、内心の存在を示します。

三角形の内心

三角形のそれぞれの角の二等分線について、次のような性質があります。

まずは、名前を付けていきましょう。三角形 ABC において、$\angle \mathrm{B}, \angle \mathrm{C}$ の二等分線をひきます。これらの角は $180^{\circ}$ より小さいので、2つの二等分線は必ず交わります。

この二等分線同士の交点を $\mathrm{I}$ とします。

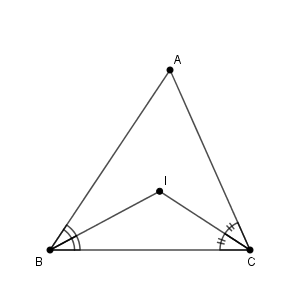
内角の二等分線は3本ひけます。2本が交わることはわかりますが、3本が交わるかどうかは明らかではありません。これを示していきます。

$\mathrm{I}$ から、辺 $\mathrm{BC, CA, AB}$ に下した垂線の足を $\mathrm{D, E, F}$ とします。

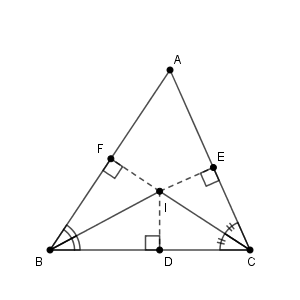
このとき、先ほど示した角の二等分線の性質から\[ \mathrm{ID=IF},\ \mathrm{ID=IE} \]が成り立ちます。これより、 $\mathrm{IE=IF}$ が成り立つので、再び、先ほど示した角の二等分線の性質を使うと、点 $\mathrm{I}$ が $\angle \mathrm{A}$ の二等分線上にあることがわかります。

このことから、三角形のそれぞれの角の二等分線はどれも $\mathrm{I}$ を通るので、1点で交わることが示せました。

内接円と内心

先ほど、三角形の3つの内角の二等分線が1点で交わることを見ました。この点は、各辺からの距離が等しいことがわかります。そのため、この点を中心として、すべての辺に接する円をかくことができます。

この円を、内接円(incircle) といいます。三角形の「内で接する円」ということですね。また、内接円の中心のことを、内心(incenter) といいます。先ほど示したことは、この内心が存在すること、内接円がかけることの証明だったわけです。

おわりに

ここでは、三角形の内心について見てきました。3つの内角の二等分線が1点で交わり、内接円がかけることを見ました。