【基本】三角形の外心
ここでは、三角形の外接円や外心について見ていきます。
垂直二等分線
三角形の外心の話をする前に、垂直二等分線についておさらいをしておきましょう。
線分 AB があったとき、 AB の中点を通り、 AB と垂直に交わる線のことを、線分 AB の垂直二等分線(perpendicular bisector) といいます。
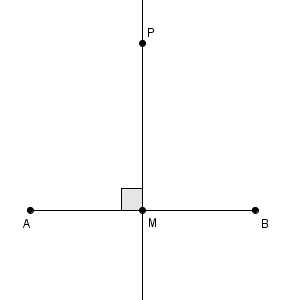
上の図で、線分 AB の中点を M としたとき、直線 PM が垂直二等分線になります。
なお、 $\mathrm{ AM=BM }$, PM が共通、 $\angle \mathrm{ PMA }=\angle \mathrm{ PMB }=90^{\circ}$ だから、三角形 APM と三角形 BPM は合同です。よって、 $\mathrm{ AP=BP }$ が成り立ちます。
逆に、 $\mathrm{ AP=BP }$ なら、 P から AB に下した垂線の足を $\mathrm{ M }'$ とした場合、 $\mathrm{ AP=BP }$, $\mathrm{PM'}$ 共通、 $\angle \mathrm{ PM'A }=\angle \mathrm{ PM'B }=90^{\circ}$ なので、三角形 $\mathrm{ APM' }$ と三角形 $\mathrm{ BPM' }$ は合同です。よって、 $\mathrm{ AM'=BM' }$ が成り立つから、 P は AB の垂直二等分線上にあることがわかります。
以上から、次の性質が言えます。
このことを使えば、外心の存在が簡単に言えます。
三角形の外心
三角形の各辺の垂直二等分線について、次のような性質があります。
この点を外心といいます。以下では、この点の存在について示していきます。
まずは、名前を付けていきましょう。三角形 ABC において、辺 AB, AC の垂直二等分線をひきます。これらは必ず交わります。なぜなら、もし交わらなければ、垂直二等分線同士が平行ということになり、これらに垂直な辺 $\mathrm{AB}, \mathrm{AC}$ 同士も平行になってしまうからです。
この垂直二等分線同士の交点を $\mathrm{O}$ とします。
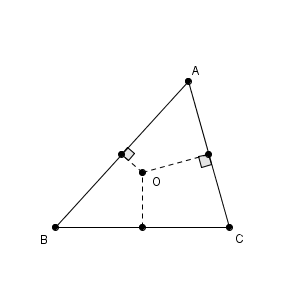
2本の垂直二等分線が交わることはわかりますが、3本が交わるかどうかは明らかではありません。そこで、これを示していきます。辺 $\mathrm{BC}$ の垂直二等分線が $\mathrm{O}$ を通れば、3本の垂直二等分線が1点で交わることが示せたことになります。
さて、先ほど見た垂直二等分線の性質により、 O は、辺 AB の垂直二等分線上にある点だから\[ \mathrm{ OA=OB } \]が成り立ちます。また、 O は、辺 AC の垂直二等分線上にもある点だから\[ \mathrm{ OA=OC } \]が成り立ちます。よって、\[ \mathrm{ OB=OC } \]であることがわかります。
このことから、再び垂直二等分線の性質より、 O は、辺 BC の垂直二等分線上にあることがわかります。
よって、三角形の各辺の垂直二等分線が1点で交わることが示せました。
外接円と外心
先ほど、各辺の垂直二等分線が1点で交わることを見ました。この点は、各頂点からの距離が等しいことがわかります。そのため、この点を中心に、すべての頂点を通る円をかくことができます。

この円を、外接円(circumcircle) といいます。三角形の「外で接する円」ということですね。また、外接円の中心のことを、外心(circumcenter) といいます。先ほど示したことは、この外心が存在すること、外接円がかけることの証明だったわけです。
なお、どんな三角形でも、外接円をかくことができますが、外心がどこにあるかは、三角形の形によって異なります。上の例は鋭角三角形です。直角三角形の場合は、斜辺上に外心が来ます。鈍角三角形の場合は、次のようになります。
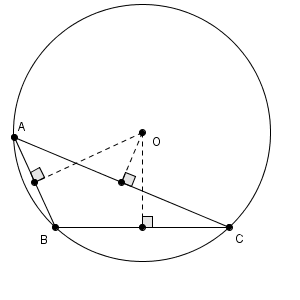
おわりに
ここでは、三角形の外心について見てきました。各辺の垂直二等分線が1点で交わり、外接円がかけることを見ました。





