【基本】正負の数の減法
ここでは、正の数や負の数の減法(引き算)について見ていきます。加法(足し算)に比べると、少しわかりづらいです。【導入】気温と負の数の引き算の内容も見ておくと、いいかもしれません。
引き算って何だっけ?
正の数や負の数の加法(足し算)について見たので、今度は引き算について考えていきましょう。
そもそも、今まで、どういうときに引き算を使っていたでしょうか。例えば、「みかんが8個あって、3個食べたら何個残りますか」という問題があれば、\[ 8-3=5 \]と計算しますね。

3個「減る」ことを表すのに、引き算を使っていました。
また、こういう問題もあったでしょう。「みかんをいくつか持っていました。ある人から3個追加でもらったので、合計で8個になりました。はじめに何個持っていましたか」。こういう場合にも、引き算を使いました。同じ式である\[ 8-3=5 \]で計算しますね。
「どんな数に3を足せば、8になるか」を求めるのに、引き算を使っていました。
こうした考えを踏まえて、正の数や負の数を引く方法について考えてみましょう。なお、引き算のことを、減法(げんぽう、subtraction)とか減算といいます。引き算の結果を差(difference) といいます。
正の数から正の数を引く場合
正の数から正の数を引く計算は、小学校でもやっていました。 $(+8)-(+3)$ は、 $8-3$ と同じことなので、 $5$ だとわかります。
ただ、中学の数学では、 $(+3)-(+8)$ というような計算も出てきます。これは、どう考えればいいでしょうか。
先ほどみた引き算の例のうち、「減ることを引き算で表す」という発想では考えにくいですね。3個しかみかんがないのに、8個食べることはできません。8個減らすことができませんね。
一方、後者の例、「どんな数に○を足せば、□になるか」という発想ではどうでしょうか。今の場合、 $+8$ を引くのだから、「どんな数に $+8$ を足せば、 $+3$ になるか」と考えてみましょう。数直線で考えると、次のようになります。
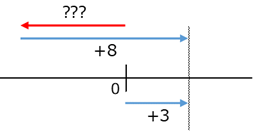
上の図の赤い線のように動いてから、右へ $8$ 移動すると、最終的に、右へ $3$ 移動した点に移ります。つまり、左へ $5$ 移動すればいいのですね。だから、\[ (+3)-(+8)=-5 \]と考えることができます。負の数を学んだので、小さい数から大きな数を引く計算もできるようになりました。
上の数直線の図を見ると、右へ $3$ 移動した点から、左へ $8$ 移動した点に移っていることがわかります。なので、 $(+8)$ を引くことは、左へ $8$ 移動することと同じだ、とも考えられます。
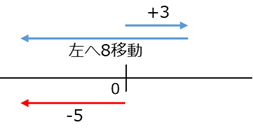
小学校では、「どんな数に○を足せば、□になるか」を考えるときに、引き算を使いました。この発想を使えば、負の数が出てくる場面でも、差が求められる、というわけです。「個数が減る」という発想では考えにくいので、数直線を使って考えていきましょう。
負の数から正の数を引く場合
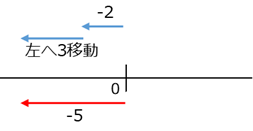
同じように、負の数から正の数を引く場合も考えることができます。\[ (-2)-(+3) \]であれば、「どんな数に $+3$ を足せば、 $-2$ になるか」を考えればいいですね。
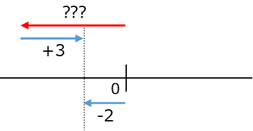
数直線で考えると、左へ $5$ 移動しておけばいいので、 $-5$ だということがわかります。\[ (-2)-(+3)=-5 \]というわけです。
図をよく見ると、左へ $2$ 移動した点から、さらに左へ $3$ 移動した点に移っていることがわかります。なので、 $(+3)$ を引くことは、左へ $3$ 移動することと同じだ、とも考えられます。
負の数を引く場合
ここまで、正の数を引く場合を見てきましたが、このケースは考えやすい結果ではないかと思います。結局、 $+3$ を引くというのは、数直線上で、左へ $3$ 移動することと同じだ、と気づくでしょう。
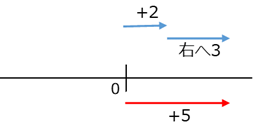
しかし、負の数を引く場合は、少し難易度が上がります。\[ (+2)-(-3) \]を考えてみましょう。これも、ここまで考えていたように、「どんな数に $-3$ を足せば、 $+2$ になるか」を考えてみます。 $-3$ を足すことは、左へ $3$ 移動することに対応します。移動した結果、 $+2$ の点に移動していると考えると、図は次のようになります。
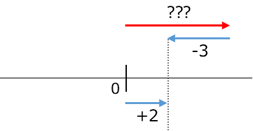
数直線で考えると、右へ $5$ 移動しておけばいいことがわかるので\[ (+2)-(-3)=5 \]となります。
図をよく見ると、 $(-3)$ を引くというのは、右へ $3$ 移動すること、と同じだ、ということがわかります。
ここまでのことを踏まえて、実際に計算してみましょう。
(1) $(+4)-(+6)$
(2) $(-4)-(+6)$
(3) $(+4)-(-6)$
数直線で考えてみましょう。(1)は、何に $+6$ を足すと $+4$ になるか、を考えます。
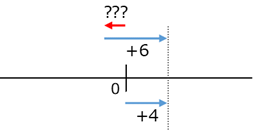
上の図から、 $(+4)-(+6)=-2$ と計算できます。
(2)は、何に $+6$ を足すと $-4$ になるか、を考えます。
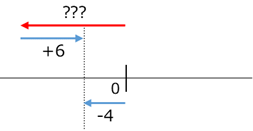
上の図から、 $(-4)-(+6)=-10$ と計算できます。
(3)は、何に $-6$ を足すと $+4$ になるか、を考えます。
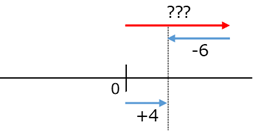
上の図から、 $(+4)-(-6)=10$ と計算できます。
おわりに
ここでは、正の数や負の数を用いた減法について見てきました。「□-○」を、「何に○を足せば、□になるか」と考え、数直線を用いて考えました。ただ、毎回、数直線を使うのは大変ですね。別のページでは、数直線を使わずに引き算を行う方法を見ていきます。





