【基本】散布図
ここでは、2つのデータの関係を調べるときに使える、散布図を紹介します。また、散布図が使いにくいときに利用できる、相関表も紹介します。
散布図
例えば、ある30人のクラスで、英語と数学の小テストをしたとします。両方とも50点満点だったとします。この2つのデータを見て、「英語の成績がよかった人は、数学の成績もよかったのではないか」という予想を確かめたい場合、どうするのがいいでしょうか。
おそらく、点数を一覧にして眺めてみても、よくわからないと思います。そこで、よくある方法ですが、これをグラフにしよう、という発想が出てきます。
2つのデータの関係を把握するためによく使われるのが散布図です。散布図(scatter plot)とは、2つのデータと平面上の点とを対応させたグラフのことです。見たほうが早いので、さっそく見てみましょう。次のグラフは、上の英語と数学の小テストの結果を散布図にしたものです。
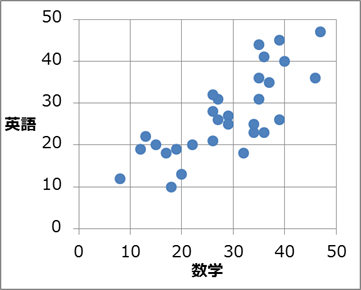
一次関数のようにまっすぐな線にはなりませんが、「英語の成績がよかった人は、数学の成績もよかった傾向がある」といえるでしょう。
相関表
散布図は、2つのデータの関係、つまり、「片方が大なら、もう片方も大」という関係や「片方が大なら、もう片方も小」といった関係を把握するのに便利です。ただ、点の数が多くなってくると、散布図は見にくくなってしまいます。もし上の小テストの結果が200人分あったら、グラフは点だらけになってしまいます。
そこで、相関表が使われることがあります。相関表(contingency table)は、2つの度数分布表を縦と横に組み合わせたものです。上の小テストの例でみると、次のようなものになります。
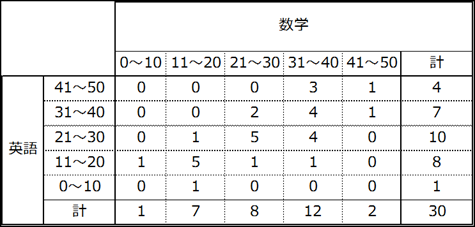
縦だけ、横だけを見ると、度数分布表です(参考:【基本】データ、度数分布表、ヒストグラム)。相関表は、これを合体させたものです。
相関表があれば、例えば散布図で点が密集していても、どこの範囲にどれくらいのデータがあるかを把握することができます。データが多い時には、散布図とともに用いることがあります。
なお、相関表は、分割表と呼ばれることもあります。
おわりに
ここでは、散布図と相関表についてみました。これらは2つのデータの関係を見るのによく使います。見方自体は難しくはないと思うので、どういうものかを知っておくだけでいいでしょう。





