【基本】二次不等式（判別式が正のとき）

ここでは、グラフを使って二次不等式を解く方法を見ていきます。グラフが x 軸と2点で交わる場合を考えます。

例題

まず(1)ですが、二次方程式のように $x\lt \pm 2$ とすることはできません。 $x\lt -2$ の値を考えれば、 $x^2\lt 4$ を満たさないので、間違いだとわかります（そもそもこんな書き方はありません）。

このような二次不等式は、 $x^2-4 \lt 0$ と変形してから、 $y=x^2-4$ のグラフをかいて考えるとわかりやすくなります。 x 軸上の点の y 座標は0なので、グラフが x 軸よりも下に来る範囲を求めればいいからです。このような考え方は、【基本】一次不等式と一次関数のグラフで紹介しています。

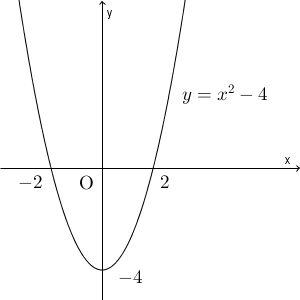
グラフは上のようになります。$x^2-4=0$ の解は $x=\pm 2$ なので、x 軸との交点もグラフ中にあるとおりです。

ここで、 $x^2-4 \lt 0$ となるのは、 $y=x^2-4$ のグラフが x 軸より下にある範囲なので、グラフから $-2\lt x \lt 2$ となることがわかります。これが答えとなります。

例題のつづき

次は(2)です。これも(1)と基本的な流れは同じです。

このまま考えてもいいのですが、 $x^2$ の係数が負なので、全体に $-1$ を掛けておいた方が分かりやすくなると思います。\[ x^2-2x-2 \geqq 0 \]を考えます。

まず、 $y=x^2-2x-2$ と x 軸との交点を求めておきましょう。解の公式から次のようになります。
\begin{eqnarray} x &=& \frac{-(-2)\pm\sqrt{(-2)^2-4\times(-2)} }{2} \\ &=& 1\pm\sqrt{1+2} \\ &=& 1\pm\sqrt{3} \\ \end{eqnarray}このことから、グラフをかくと次のようになります。

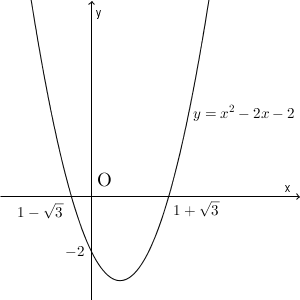
このグラフから、 $x^2-2x-2 \geqq 0$ の範囲を考えるには、グラフが x 軸上かそれより上にあればいいので、答えは次のようになります。\[ x\leqq 1-\sqrt{3}, \quad x\geqq 1+\sqrt{3} \]2つの区間が答えになります。

おわりに

ここでは、二次関数のグラフが下に凸で x 軸と2点で交わっているとき（判別式 D が正のとき）の、二次不等式について見てきました。また、上に凸の場合は、不等式にマイナスを掛けて、下に凸になるようにしました。

このときの答えを一般的にまとめると、次のようになります。

この一覧は覚える必要はありません。グラフをかいて考えられるようにしておきましょう。