【基本】二次不等式（判別式が0のとき）

ここでは、【基本】二次不等式（判別式が正のとき）に引き続き、グラフを使って二次不等式を解く方法を見ていきます。グラフが x 軸と接する場合を考えます。

例題

【基本】二次不等式（判別式が正のとき）と同じように、グラフをかいて x 軸との位置関係で考えます。

不等式の左辺は次のように変形できます。\[ x^2+4x+4=(x+2)^2 \]このことから、 $y=x^2+4x+4$ のグラフは次のようになります。

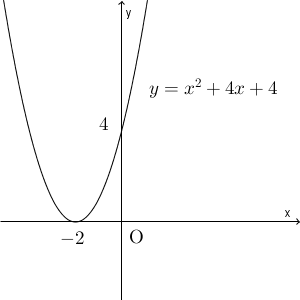
放物線は、点 $(-2,0)$ で x 軸に接します。

さて、まずは(1)の $x^2+4x+4 \geqq 0$ を考えてみます。左辺がグラフ上の点、右辺が x 軸上の点に対応するので、グラフ上の点が x 軸上の点かそれより上にある範囲が答えになります。

ただ、今の場合、全範囲でその条件を満たしているんですよね。 $x=-2$ のときは x 軸上にあり、それ以外は x 軸より上にあるからです。つまり、このときの答えは「すべての実数」となります。少し変わった答えですね。

(2)は、 $x^2+4x+4 \gt 0$ です。今回は、 x 軸より上の部分だけが答えです。つまり、 $x=-2$ は外さないといけない、ということです。これ以外ではグラフは x 軸より上にあるので、答えは「 $-2$ 以外のすべての実数」となります。

同じグラフですが、もう一度載せます。

(3)は、 $x^2+4x+4 \lt 0$ です。これは、 x 軸より下の部分に対応します。が、そんな範囲はありません。なので、「ない」が答えになります。 x 軸より下になることがないんだから、「ない」となります。

最後に、(4)の $x^2+4x+4 \leqq 0$ です。この場合は、 x 軸上の点かそれより下にある範囲が答えになります。グラフが x 軸より下にくることはないのですが、 x 軸上に来ることはあります。 $x=-2$ のときですね。よって、答えは「 $x=-2$ 」となります。不等式の解なのに、答えが1つだけになるんですね。

全体的に、変わった答えですね。普通の一次不等式では出会わない答えばかりです。

おわりに

ここでは、二次関数のグラフが下に凸で x 軸と接しているとき（判別式 $D=0$ のとき）の、二次不等式について見てきました（なお、上に凸の場合は、不等式にマイナスを掛ければ、下に凸になります）。

このときの答えを一般的にまとめると、次のようになります。

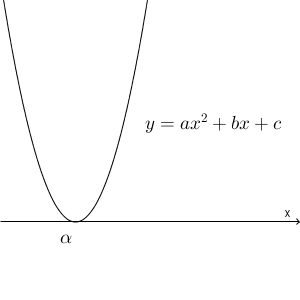
この一覧は覚える必要はありません。グラフをかいて考えられるようにしておきましょう。