【基本】空間における2平面の位置関係

ここでは、空間における2平面の位置関係や、なす角について見ていきます。

空間における2平面の位置関係

空間において、異なる2つの平面があったときに、どのような位置関係があるかを考えてみます。

まずは直線のときと同じように、1つも共有点がない場合が考えられます。

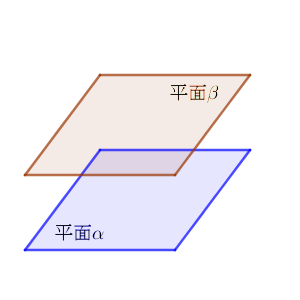
（平面 $\alpha$ の上に平面 $\beta$ が浮いている、という図です）

このような場合に、2つの平面は平行(parallel) である、といいます。

これ以外に、共有点がある場合も考えられます。この場合は、次のようになります。

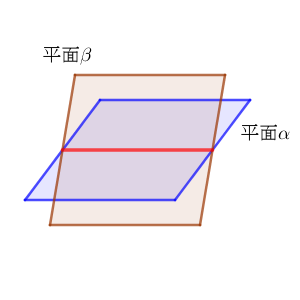
この場合は、交わる(intersect) といいます。

異なる2つの平面が共有点をもつときは、この2平面は、ある1つの直線を共有します。例えば、水面に下敷きをつける場面を想像してみましょう。下敷きを見てみると、空気中と水中の境い目は直線で区切られていることがわかるでしょう。

異なる2つの平面 $\alpha,\beta$ があった場合、平行か交わるか、どちらかのケースしかありません。平行の場合は、 $\alpha /\!/ \beta$ と表します。交わる場合はある1つの直線を共有しますが、この直線のことを交線(line of intersection) といいます。

2平面のなす角

次のような直方体を考えてみます。

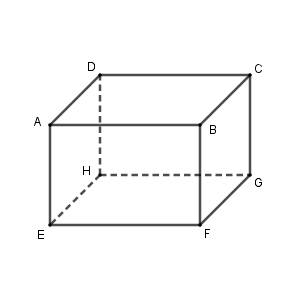
このとき、下の面 $\mathrm{EFGH}$ と左の面 $\mathrm{ADHE}$ を考えてみましょう。この2つの面は交わっています。が、もっというと、垂直のように感じられます。

異なる2つの平面に対しても、2直線のときのように、なす角を考えられないでしょうか。

パッと思いつく方法としては、それぞれの平面に含まれる直線を考えて、その2直線のなす角を使う、というものがあるでしょう。しかし、使う直線が適当だとよくないことが起こってしまいます。

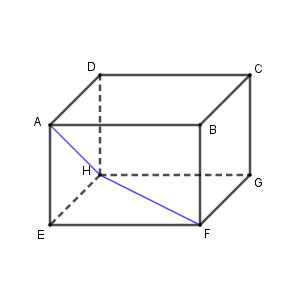
例えば、平面 $\mathrm{EFGH}$ と平面 $\mathrm{ADHE}$ について考えているときに、直線 $\mathrm{HF}$ と直線 $\mathrm{AH}$ を選んできたとしましょう。この2直線のなす角は $90^{\circ}$ ではありません。他にもいろんな直線が考えられますが、直線のとり方によって角の大きさが変わってしまいます。

そこで、とり方によって角の大きさが変わらないように、次のようにしてみましょう。交線 $\mathrm{EH}$ 上に点 $\mathrm{O}$ をとり、平面 $\mathrm{EFGH}$ 、平面 $\mathrm{ADHE}$ 上で、 $\mathrm{O}$ を通り、交線に対して垂直な直線を引きます。

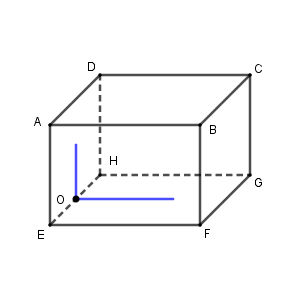
こうしてから2直線のなすを考えれば、点 $\mathrm{O}$ をどこにとったとしても、垂直になります。

このことを踏まえ、2平面のなす角は、次のように定義します。

図で表すと次のようになります。ノートパソコンを開いた状態を想像しながら図を見てください。

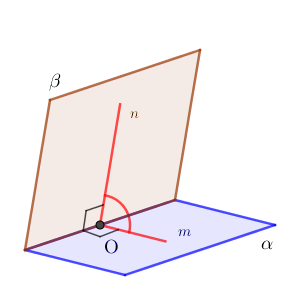
2平面のなす角を定義するには、厳密には、点 $\mathrm{O}$ のとりかたによって角の大きさが変わらないことを示す必要があります。その証明はこの記事の後半で行います。

2平面 $\alpha,\beta$ のなす角が $90^{\circ}$ のとき、 $\alpha$ と $\beta$ は垂直であるといいます。直交するともいいます。記号では、 $\alpha\perp\beta$ と表します。

一般的に、2平面のなす角は $90^{\circ}$ 以下の大きさで表します。

2平面のなす角が定義できることについて

ここからは、2平面のなす角が定義できることを確認します。つまり、上の定義に出てきた点 $\mathrm{O}$ のとり方によって、角の大きさが変わらないことを確認します。これが言えないと、2平面のなす角を1つに決めることができません。（よくわからない場合は、このセクションは飛ばしても大丈夫です）

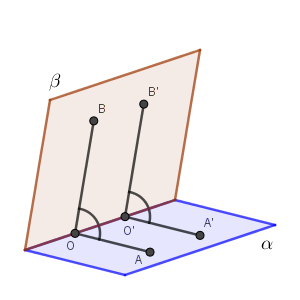
上の図のように、2つの平面 $\alpha,\beta$ が交わっているとします。交線上に点 $\mathrm{O},\mathrm{O'}$ をとって、平面 $\alpha,\beta$ 上で、交線と垂直に交わる直線をひきます。

さらに、交線と垂直に交わる直線上で、 $\mathrm{OA}=\mathrm{O'A'}$ を満たすように点 $\mathrm{A,A'}$ を平面 $\alpha$ 上にとり、 $\mathrm{OB}=\mathrm{O'B'}$ を満たすように点 $\mathrm{B,B'}$ を平面 $\beta$ 上にとることにします。

このときに、もし $\angle \mathrm{AOB}=\angle \mathrm{A'O'B'}$ が示せたとすると、交線上のどんな好きなところに $\mathrm{O}$ をとっても角が一定であることがわかるので、2平面のなす角がきちんと定義できることがわかります。

それでは、$\angle \mathrm{AOB}=\angle \mathrm{A'O'B'}$ を示していきましょう。

今、平面 $\alpha$ 上で、 $\mathrm{OA}$ も $\mathrm{O'A'}$ も交線に対して垂直なので、2直線は平行です。1組の辺が等しくで平行なので、四角形 $\mathrm{OAA'O'}$ は平行四辺形だとわかります（長方形であることもいえます）。

同様にして、四角形 $\mathrm{OBB'O'}$ も平行四辺形だといえます。

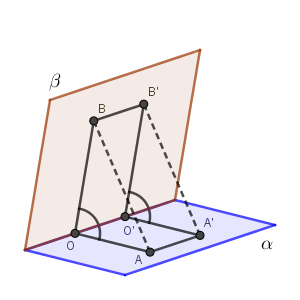
このことから、まず $\mathrm{AA'}=\mathrm{OO'}=\mathrm{BB'}$ がわかります。また、 $\mathrm{AA'} /\!/\mathrm{OO'}$, $\mathrm{OO'} /\!/\mathrm{BB'}$ より、$\mathrm{AA'} /\!/\mathrm{BB'}$ がわかります（参考：【応用】空間における平行な3直線）。以上から、四角形 $\mathrm{AA'B'B}$ も平行四辺形だとわかります。

これより、 $\mathrm{AB}=\mathrm{A'B'}$ がわかります。また、 $\mathrm{OA}=\mathrm{O'A'}$ と $\mathrm{OB}=\mathrm{O'B'}$ （こうなるように点をとっていたので）より、 $\triangle \mathrm{OAB}\equiv\triangle\mathrm{O'A'B'}$ だとわかります。

こうして、 $\angle \mathrm{AOB}=\angle \mathrm{A'O'B'}$ となることがわかりました。交線上にどのように点 $\mathrm{O}$ をとっても、なす角が変わらないので、2平面のなす角がちゃんと定義できることがわかりました。

おわりに

ここでは、空間における2平面の位置関係や、なす角について見てきました。なす角は、交線に対して垂直な直線で考える点をおさえておきましょう。