【基本】空間における2直線の位置関係

ここでは、空間における2直線の位置関係や、なす角について見ていきます。

空間における2直線の位置関係

平面の場合、異なる2直線があれば、交わるか平行かのどちらかしかありません。

空間の場合にも、交わる、平行というケースがあります。空間の場合には、さらにもう一つ、ねじれ(skew) という状況があります。ねじれとは、次のような状況です。

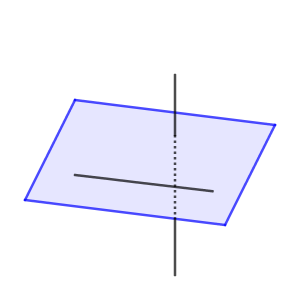
上の図では2直線の一部しかかいていませんが、伸ばしていっても交わることはありません。かといって、平行というわけでもないですね。

平行の場合もねじれの場合も、2直線は交わりません。では違いは何かというと、同一平面上にあるかどうかです。2直線が共有点をもたない場合、2直線が同一平面上にある場合は平行、同一平面上にない場合はねじれ、です。

例えば、次のような直方体があったとしましょう。

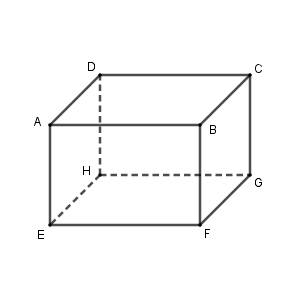
このとき、辺 $\mathrm{AB}$ に平行な辺は、次の3つです。

• 辺 $\mathrm{CD}$
• 辺 $\mathrm{EF}$
• 辺 $\mathrm{GH}$

辺 $\mathrm{AB}$ とねじれの位置にある辺は、次の3つです。

• 辺 $\mathrm{CG}$
• 辺 $\mathrm{DH}$
• 辺 $\mathrm{EH}$
• 辺 $\mathrm{FG}$

他の4つの辺は、辺 $\mathrm{AB}$ と交わっています。特に、垂直に交わっていることもわかります。

平行かつ平行なら平行？

空間において、3つの直線 $\ell,m,n$ が、次の条件を満たしていたとします。\[ \ell /\!/ m,\ m /\!/ n \]このとき、次は成り立つでしょうか。\[ \ell /\!/ n \]

文章で書くと、 $\ell$ と $m$ が平行で、 $m$ と $n$ が平行なら、 $\ell$ と $n$ も平行であるか、ということです。

これは平面のときには成り立ちますが、空間のときも同じように成り立ちます。証明は難しいので、教科書でも証明なしで紹介していることが多いです。当サイトでは、【応用】空間における平行な3直線を参照してください。

2直線のなす角

2直線が交わっている場合、なす角を考えることができますね。平行の場合は、交わらないので角を考えることはできません。では、ねじれの場合でどうでしょうか。

例えば、次の図の辺 $\mathrm{AB}$ と辺 $\mathrm{DH}$ について考えてみましょう。

交わっていないので、そのままではなす角を考えることはできません。そこで、平行移動して交わるようにしてみるとどうでしょうか。

平行移動をして交わるようにするには、いろいろなケースが考えられます。

• 辺 $\mathrm{DH}$ を辺 $\mathrm{AE}$ に移動する
• 辺 $\mathrm{DH}$ を辺 $\mathrm{BF}$ に移動する
• 辺 $\mathrm{AB}$ を辺 $\mathrm{DC}$ に移動する

他にも考えられますが、どのように平行移動をしても、 $90^{\circ}$ で交わることがわかります。

これを踏まえると、交わるように平行移動してから考えればよさそうだ、と予想できます。

ただ、注意が必要なのは、平行移動の仕方によって角度がかわってしまうことがないか、という点です。実は、どのように平行移動してもいいことが知られています（参考：【応用】空間における2直線のなす角）。

2直線 $\ell,m$ のなす角が $90^{\circ}$ のとき、$\ell$ と $m$ は垂直であるといいます。直交する、ともいいます。また、記号では $\ell \perp m$ と表します。

2直線のなす角は、一般的に、 $90^{\circ}$ 以下の大きさで表します。

垂直かつ垂直なら平行？

空間において、3つの直線 $\ell,m,n$ が、次の条件を満たしていたとします。\[ \ell \perp m,\ m \perp n \]このとき、次は成り立つでしょうか。\[ \ell /\!/ n \]

平面で考えている場合は成り立ちますが、空間の場合には成り立ちません。例えば、先ほどの直方体の例を見てみましょう。

辺 $\mathrm{AB}$ と辺 $\mathrm{AD}$ は垂直に交わっています。辺 $\mathrm{AB}$ と辺 $\mathrm{AE}$ も垂直に交わっています。しかし、辺 $\mathrm{AD}$ と辺 $\mathrm{AE}$ は平行ではありませんね。

「平行かつ平行なら平行」は成り立ちましたが、「垂直かつ垂直なら平行」は成り立ちません。平面の世界で成り立つことも空間の世界では成り立たないことがあります。いろんなケースを想像して、反例がないか考えるようにしましょう。

おわりに

ここでは、空間における2直線の位置関係や、なす角について見てきました。平面で成り立つことも空間では成り立たないこともある、ということを把握しておきましょう。