【基本】空間における直線と平面の位置関係
ここでは、空間における直線と平面の位置関係や、垂直について見ていきます。
空間における直線と平面の位置関係
空間において、直線 $\ell$ と平面 $\alpha$ があったときに、どのような位置関係があるかを考えてみます。共有点の個数に着目して考えていきます。
まず、共有点が1点もない場合があります。

この場合、 $\ell$ と $\alpha$ は平行であるといいます。記号では、 $\ell /\!/ \alpha$ と書きます。
次に、共有点を1点だけもつ場合があります。

この場合、 $\ell$ と $\alpha$ は交わる、といいます。
最後に、共有点を2点以上もつ場合があります。

共有点が2点あれば、直線 $\ell$ は平面 $\alpha$ 上にあることになります。
共有点の個数によって分けると、平行、交わる、直線が平面上にある、の3パターンがあることがわかります。
直線と平面の垂直
先ほど、直線と平面の位置関係は、3種類あることを見ました。この中の「交わる」場合には、特に重要なケースがあります。それは「垂直」です。
例えば、四角錐の体積を求める場合、ある点から底面に向かって垂線をひいて、高さを考えていました。
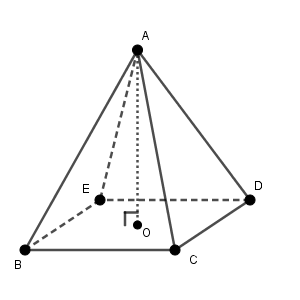
よく考えると、小学校や中学校で、この垂線の説明はちゃんとしなかったかもしれませんが、高校数学ではちゃんと定義します。でも、直線と平面の垂直は、どう定義すればいいのでしょうか。
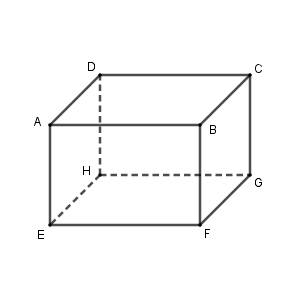
例えば、平面上の1つの直線と垂直、なだけではダメです。例えば次の図を見てみましょう。

下の面 $\mathrm{EFGH}$ を考えてみます。このとき、 $\mathrm{AF}$ と下の面上にある直線 $\mathrm{FG}$ とは垂直に交わります。しかし、 $\mathrm{AF}$ が下の面に垂直だ、とはいわないでしょう。
ということはもっと他にも条件が必要だとわかります。実は、1本じゃなく、平面上にあるあらゆる直線を持ち出して、次のように定義します。
$\ell$ と $\alpha$ が垂直であることを、 $\ell$ と $\alpha$ は直交する、ともいいます。記号では $\ell\perp\alpha$ と書きます。
このように定義すると、たしかに先ほどの直方体の例だと、下の面に垂直な辺は $\mathrm{AE}$ など、今まで直感的に考えてきた「垂直」のイメージと一致していることがわかります。
とはいえ、「あらゆる直線」は少し多すぎる気がします。「直線と平面が垂直に交わっているかどうか」を調べたいときに、平面上の直線全部を持ち出してこないといけないなら、調べるのが大変ですね。
実は、次のことが知られています。
つまり、定義上は「あらゆる直線」となっていますが、実際は、2本調べればOKということです。
この証明は大変で、教科書でも載っていないことがほとんどです。このサイトでは、【応用】平面に垂直な直線に記載しています。
平面 $\alpha$ 上にない点 $\mathrm{P}$ について、点 $\mathrm{P}$ を通り、 $\alpha$ に垂直な直線がただ1つあります。この直線のことを、点 $\mathrm{P}$ から $\alpha$ に下した 垂線(perpendicular line) といいます。
これらを踏まえ、次の問題を考えてみましょう。
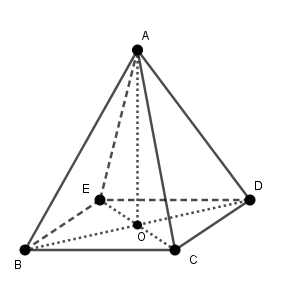
条件からわかることとして、まず、正四角錐ということから、 $\mathrm{AB=AC}$ があります。また、底面は正方形なので、 $\mathrm{OB=OC}$ がわかります。 $\mathrm{AO}$ は共通なので、 $\triangle\mathrm{OAB}\equiv\triangle\mathrm{OAC}$ がわかります。
同様に、 $\triangle\mathrm{OAD}$, $\triangle\mathrm{OAE}$ とも合同だとわかります。これより、 $\mathrm{AO\perp OB}$, $\mathrm{AO\perp OC}$ といえるので、平面 $\mathrm{BCDE}$ 上の平行でない2直線と垂直なので、 $\mathrm{AO}$ が平面 $\mathrm{BCDE}$ と垂直であることがわかります。
おわりに
ここでは、空間における、直線と平面の位置関係を見てきました。垂直のケースは、立体の高さにも関連してくる内容です。





