【基本】座標空間における点

ここでは、空間ベクトルを見ていく前に、座標軸に垂直な平面の方程式、内分点や外分点、2点間の距離を見ていきます。

座標軸に垂直な平面の方程式

【基本】空間の座標 で、点 $\mathrm{P}$ を通る、 $x$ 軸に垂直な平面が出てきました。

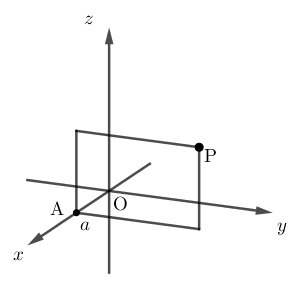
図で表すと平面の一部分のようになってしまうのですが、上下左右に無限に広がっていると考えてください。

この平面（ $\mathrm{P,A}$ がある平面）上の点の座標には、ある特徴があります。それはどんな点でも、 $x$ 座標が $a$ である、というものです。逆に、 $x$ 座標が $a$ なら、この平面上にあります。

なので、この平面の方程式は $x=a$ となります。平面 $x=a$ とかけば、点 $(a,0,0)$ を通る、 $x$ 軸に垂直な平面を表します。

同様に、以下のようになります。

慣れるまではこれが平面の方程式だと思えないかもしれませんが、空間で条件を満たす点を集めたらどうなるか、と考えれば、平面をイメージしやすいと思います。

なお、平面 $x=0$ は $yz$ 平面を表します。平面 $y=0$ は $zx$ 平面、平面 $z=0$ は $xy$ 平面を表します。

内分点・外分点

【基本】平面上での内分点と外分点 でも見たように、線分 $\mathrm{AB}$ を $m:n$ に内分する点とは、線分 $\mathrm{AB}$ 上で、 $\mathrm{AP:PB}=m:n$ を満たす点です。また、線分 $\mathrm{AB}$ を $m:n$ に外分する点とは、線分 $\mathrm{AB}$ の延長線上で、 $\mathrm{AP:PB}=m:n$ を満たす点です。この定義は、空間でも同じです。

では、内分点・外分点の座標がどうなるかを考えます。

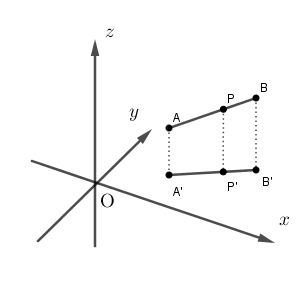
$\mathrm{A}(x_1,y_1,z_1)$, $\mathrm{B}(x_2,y_2,z_2)$ とし、 $\mathrm{P}$ は線分 $\mathrm{AB}$ を $m:n$ に内分する点とします。

$\mathrm{A,B,P}$ から $xy$ 平面の垂線を下ろし、その足を $\mathrm{A',B',P'}$ とします。 $\mathrm{A',B',P'}$ は $xy$ 平面上にあり、 $\mathrm{A'P':P'B'}=m:n$ なので、平面のときの結果がそのまま使えます。 $z$ 座標は $0$ だから、 $\mathrm{P'}$ の座標は\[ \left(\frac{nx_1+mx_2}{m+n}, \frac{ny_1+my_2}{m+n}, 0 \right) \]となります。この $x$ 座標と $y$ 座標は、点 $\mathrm{P}$ の $x$ 座標と $y$ 座標とそれぞれ同じになります。

同様に、$\mathrm{A,B,P}$ から $yz$ 平面の垂線を下ろして、平面上の内分点の座標を考えれば、 $\mathrm{P}$ の $z$ 座標は\[ \frac{nz_1+mz_2}{m+n} \]になることがわかります。外分点も同じようにすると、次の結果が得られます。

平面のときの連想で結果は想像できると思います。

特に、中点の場合は\[ \left(\dfrac{x_1+x_2}{2}, \dfrac{y_1+y_2}{2}, \dfrac{z_1+z_2}{2}\right) \]となります。これもよく使います。

2点間の距離

次のような状況を考えます。

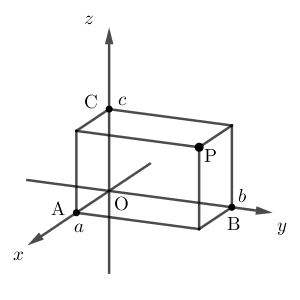
点 $\mathrm{P}(a,b,c)$ を通り、各座標軸に垂直な平面を追加しています。このとき、 $\mathrm{OP}$ 間の距離はどうなるでしょうか。

この距離は、次のように線をひくとわかりやすくなります。

こうすると、 $\mathrm{OP}=\sqrt{\mathrm{OC}^2+\mathrm{CP}^2}$ であることがわかります。また、 $\mathrm{CP}=\sqrt{\mathrm{OA}^2+\mathrm{OB}^2}$ であることから、\[ \mathrm{OP}=\sqrt{a^2+b^2+c^2} \]となります。

一般的には、空間内の2点間の距離は、 $x$ 座標、 $y$ 座標、 $z$ 座標の差をそれぞれ2乗して、足してルートを考えれば求められます。片方の点が原点に来るように平行移動して考えればいいですね。

これも、平面のときから連想できると思います。

おわりに

ここでは、座標空間における点にまつわるものを見てきました。座標軸に垂直な平面の方程式、内分点・外分点の座標、2点間の距離を見ました。平面のときから連想できるものが多いですね。