🏠 Home / 数学C / ベクトル

【基本】空間の座標

🕒 2024/06/26 🔄 2024/07/07

ここでは、空間ベクトルを見ていく前に、前提知識となる空間の座標について見ていきます。

📘 目次

座標軸

平面の場合、位置を表すには縦と横の2つを使えばいいですが、空間の場合は2つだけでは足りません。高さという3つ目が必要になります。

空間内で図形などを考える場合、図をかくために、基準となる3つの軸を使います。これらは互いに垂直で、1点で交わっているものを考えます。この3つの軸を $x$ 軸、 $y$ 軸、 $z$ 軸といい、3つまとめて座標軸(coordinate axis) といいます。座標軸の交点を原点 (origin) といい、 $\mathrm{O}$ で表します。

図でかくと、次のようになります。

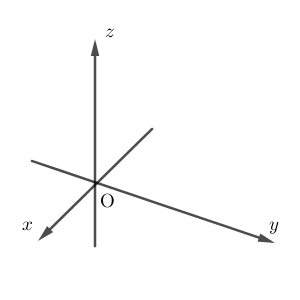
手前左側に伸びているのが $x$ 軸、右側へ伸びているのが $y$ 軸、上に伸びているのが $z$ 軸です。一方、次のような向きでかくこともあります。

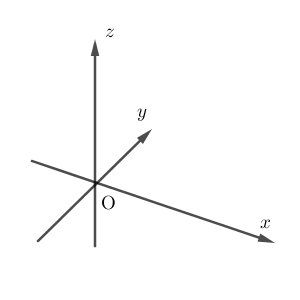
右へ伸びているのが $x$ 軸、奥へ伸びているのが $y$ 軸です。

平面の場合は、左右に伸びるのが $x$ 軸、上下に伸びるのが $y$ 軸となるようにかくのが基本ですが、空間の場合はこれと決まってはいません。考えたい状況に応じて、見やすいものを使います。

座標平面

$x$ 軸と $y$ 軸を含む平面を $xy$ 平面といいます。同様に、 $yz$ 平面、 $zx$ 平面もあります。これら3つをまとめて、座標平面(coordinate plane) と呼びます。

$x$ 軸と $yz$ 平面は垂直です。これは、 $yz$ 平面上の平行でない2直線 $y$ 軸と $z$ 軸が、どちらも $x$ 軸と垂直だからです。（参考：【基本】空間における直線と平面の位置関係）

同様に、 $y$ 軸と $zx$ 平面も垂直で、 $z$ 軸と $yz$ 平面も垂直です。

空間における点の座標

空間において、ある点 $\mathrm{P}$ があったとします。このとき、 $\mathrm{P}$ の場所を表す方法を考えます。

原点から出発し、 $x$ 軸方向、 $y$ 軸方向、 $z$ 軸方向にどのように移動すればたどりつけるか、で表せば、どの点でも表現することができるようになります。

もう少し厳密に手順を書きます。まず、 $\mathrm{P}$ を通り、 $yz$ 平面に平行な平面を考えます。この平面と $x$ 軸との交点を $\mathrm{A}$ とします。

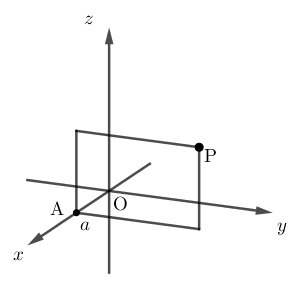
他も同様にして、各座標平面に平行な平面を考え、 $x$ 軸、 $y$ 軸、 $z$ 軸と交わる点を、 $\mathrm{A,B,C}$ とします。

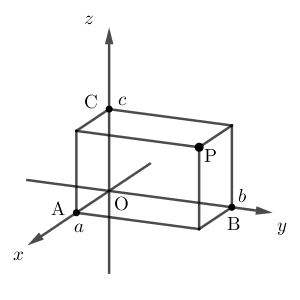
これらの点は、各座標軸上の点なので、座標軸上での座標があります。順番に $a,b,c$ とします。このとき、 $(a,b,c)$ を点 $\mathrm{P}$ の座標(coordinate) といいます。

点 $\mathrm{P}$ の座標が $(a,b,c)$ であることを、 $\mathrm{P}(a,b,c)$ と表します。平面のときと同じですね。また、 $a,b,c$ をそれぞれ $\mathrm{P}$ の $x$ 座標、 $y$ 座標、 $z$ 座標といいます。

このようにして座標を定めた空間を、座標空間(coordinate space) といいます。

なお、先ほどの図の他の点は、 $\mathrm{A}(a,0,0)$, $\mathrm{B}(0,b,0)$, $\mathrm{C}(0,0,c)$, $\mathrm{O}(0,0,0)$ となります。

また、直線 $\mathrm{PC}$ は、 $xy$ 平面に平行で、 $xy$ 平面は $z$ 軸と垂直だから、直線 $\mathrm{PC}$ と $z$ 軸は垂直です。言い換えると、直線 $\mathrm{PC}$ は、 $\mathrm{P}$ から $z$ 軸に下した垂線、ということです。