🏠 Home / 数学C / ベクトル

【基本】空間ベクトルの平行と分解

🕒 2024/07/02 🔄 2024/07/07

ここでは、空間ベクトルでの平行や、空間ベクトルの分解について見ていきます。

📘 目次

空間ベクトルの平行

【基本】空間ベクトルでも見たように、 $k\ne 0$ のとき、 $k\vec{a}$ は $\vec{a}$ とは長さが違うだけで、向きが同じか反対かのどちらかです。いずれの場合も、平行です。

逆に、$\vec{b}$ が $\vec{a}$ と平行（どちらも $\vec{0}$ ではないとします）であれば、向きが同じなら $\vec{a}$ を $\dfrac{|\vec{b}|}{|\vec{a}|}$ 倍したもの、反対なら $-\dfrac{|\vec{b}|}{|\vec{a}|}$ 倍したものと一致します。どちらにしても、 $\vec{b}=k\vec{a}$ を満たす $k$ が存在します。

まとめると、次のようになります。

ベクトルの平行

$\vec{0}$ ではない2つのベクトル $\vec{a}$, $\vec{b}$ について、次が成り立つ。
$\vec{a} /\!/ \vec{b}$ $\iff$ $\vec{b}=k\vec{a}$ となる実数 k が存在する

平面のときに見た【基本】ベクトルの平行とまったく同じ内容です。

このことは、問題を解くときに威力を発揮します。

空間ベクトルの分解

【基本】ベクトルの分解で見た通り、平面上のベクトルは、$\vec{0}$ ではなく、平行ではない2つのベクトル $\vec{a},\vec{b}$ を使って、 $s\vec{a}+t\vec{b}$ と書けるのでした。しかも、 $s,t$ は1通りに決まるのでした。

空間の場合は、明らかに2つでは足りません（ $x,y$ 軸に平行なベクトルだけで $z$ 軸に平行なベクトルは表せません）。

かといって、3つあればいいかというと、3つなら何でもいいわけではありません。例えば、3つとも $xy$ 平面上にあれば、 $z$ 軸に平行なベクトルは表せません。ざっくりとした表現ですが、もっとバラバラの方向を向いている必要があります。

空間の場合は、ベクトルの分解は次のようになります。

まず、空間内の4点 $\mathrm{O,A,B,C}$ は 同一平面上にない とします。このとき、 $\overrightarrow{\mathrm{OA}}=\vec{a}$, $\overrightarrow{\mathrm{OB}}=\vec{b}$, $\overrightarrow{\mathrm{OC}}=\vec{c}$ とします。また、空間内に別の点 $\mathrm{P}$ をとって、 $\overrightarrow{\mathrm{OP}}=\vec{p}$ とします。 $\vec{p}$ を $\vec{a}, \vec{b}, \vec{c}$ を使って表してみます。

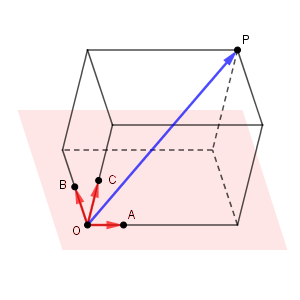
まず、 $\mathrm{O,A,B,C}$ の4点は同一平面上にはないので、 $\mathrm{O,A,B}$ の3点を含む平面は1つに決まります。この平面を、平面 $\alpha$ と呼ぶことにします。

点 $\mathrm{P}$ を通り、 $\vec{c}$ に平行な直線をひきます。 $\mathrm{C}$ は平面 $\alpha$ 上にはないので、この直線は平面 $\alpha$ と必ず1点で交わります。この点を $\mathrm{Q}$ とします。

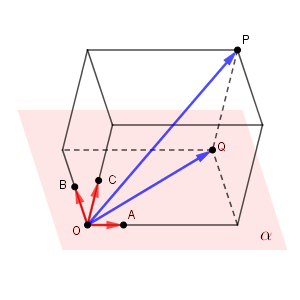
こうすると、 $\overrightarrow{\mathrm{QP}}$ と $\vec{c}$ は平行だから、 $\overrightarrow{\mathrm{QP}}=u\vec{c}$ を満たす $u$ が存在します。

また、点 $\mathrm{Q}$ は平面 $\alpha$ 上の点なので、 $\overrightarrow{\mathrm{OQ}}=s\vec{a}+t\vec{b}$ を満たす $s,t$ が存在します。（ここは平面ベクトルの結果を使っています。参考：【基本】ベクトルの分解）

以上から、 $\vec{p}=s\vec{a}+t\vec{b}+u\vec{c}$ を満たす $s,t,u$ が存在することがわかります。

また、もし存在するなら1通りしかありません。もし、 $\vec{p}=s'\vec{a}+t'\vec{b}+u'\vec{c}$ とも表せているとしたら、変形して\[ (u'-u)\vec{c}=(s-s')\vec{a}+(t-t')\vec{b} \]となります。もし $u-u'\ne 0$ なら両辺をこれで割ると、 $\vec{c}$ が $\vec{a},\vec{b}$ を使って表せることになり、 $\mathrm{O,A,B,C}$ が同一平面上にない、という条件に反してしまいます。なので、 $u-u'=0$ だから左辺は $\vec{0}$ であり、 $s=s',t=t'$ がえられます。こうして、係数の組は1通りしかないことがわかります。

ベクトルの分解（空間ベクトルの場合）

空間内の4点 $\mathrm{O,A,B,C}$ が同一平面上にはないとする。このとき、空間内の点 $\mathrm{P}$ に対し、 $s,t,u$ を使って次の形に1通りに表すことができる。\[ \overrightarrow{\mathrm{OP}} = s\overrightarrow{\mathrm{OA}}+t\overrightarrow{\mathrm{OB}}+u\overrightarrow{\mathrm{OC}} \]

このように分解できることは重要ですし、1通りに表せることも重要です。また、4点が同一平面上にない、という条件も重要です。この条件がなければ、分解できるかどうかはわかりませんし、1通りかどうかもわかりません。