【基本】放物線の焦点と準線

ここでは、放物線を図形的な観点から見ていくことにします。

放物線の定義

【基本】円の方程式で見たように、円の方程式は次のように表されます。\[ (x-a)^2+(y-b)^2=r^2 \]このグラフは、点 $(a,b)$ を中心とした半径 $r\ (\gt 0)$ の円となります。

また、図形的に言えば、円とは、「ある点から一定の距離だけ離れた点の集まり」となります。この「ある点」のことを「中心」と呼び、「一定の距離」を「半径」と呼びます。

過去には、放物線も扱いました。【標準】二次関数y=ax^2+bx+cのグラフの頂点などで見たように、次の式を「放物線の方程式」と呼ぶのでした。\[ y=ax^2+bx+c \]ただ、円のときとは違って、放物線が図形的にどのような点の集まりなのか、というのは、今まで扱っていなかったですね。

図形的には、放物線は、「ある点と、その点を通らないある直線からの距離が等しい点の集まり」で定義されます。といわれても、本当にこれが放物線になるのかどうか、パッとはわかりませんね。計算をして確かめてみましょう。

放物線の焦点と準線

この軌跡は、上で書いた「ある点と、その点を通らないある直線からの距離が等しい点の集まり」を意味しています。この軌跡上の点 $(x,y)$ が満たす方程式を考えてみましょう。

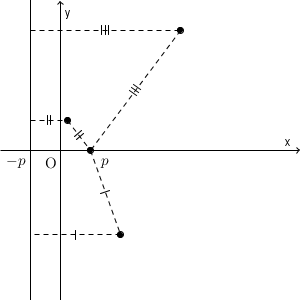
点 $(p,0)$ と点 $(x,y)$ との距離は $\sqrt{(x-p)^2+y^2}$ であり、直線 $x=-p$ と点 $(x,y)$ との距離は $|x-(-p)|$ なので、次の式が成り立ちます。\[ \sqrt{(x-p)^2+y^2}=|x+p| \]両辺とも正なので、両辺を2乗して変形すると
\begin{eqnarray} x^2-2px+p^2+y^2 &=& x^2+2px+p^2 \\[5pt] y^2 &=& 4px \\[5pt] \end{eqnarray}となります。式を逆にたどっていけば、\[ \sqrt{(x-p)^2+y^2}=|x+p| \]が成り立つことがわかるので、\[ y^2=4px \]が求める軌跡となります。

このグラフは次のようになります。

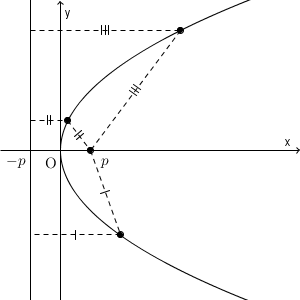
縦横を入れ替えてみればわかりますが、たしかに今まで見た放物線と一致していますね。放物線の各点が条件を満たしていることがわかりやすいように、動きをつけたものも見てみましょう。

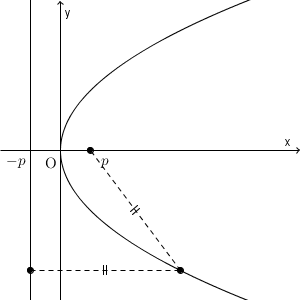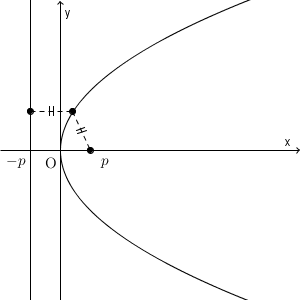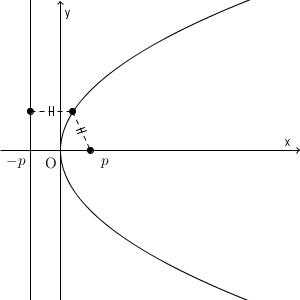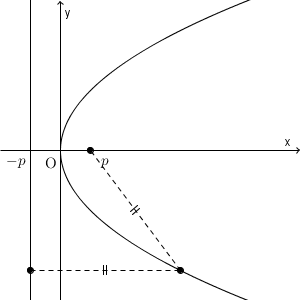
点と直線が他の場合でも（例えば直線が斜めの場合などでも）、平行移動したり回転移動してから考えれば、同じように放物線であることが確認できることがわかるでしょう。

円の場合、「中心と半径」を決めれば、どういう円かが決まります。放物線の場合は、上で見た通り、「点と直線」を決めれば、どういう放物線かが決まります。これらは、放物線を決める重要なものなので、名前がついています。点のことを焦点(focus)、直線のことを準線(directrix) といいます。

以上のことをまとめると、次のようになります。

準線に垂直な直線を、放物線の軸といいます。また、放物線と軸との交点を、放物線の頂点といいます。これらは、二次関数の分野で見たときと一致していますね。

y軸を軸とする放物線

上で見た放物線ですが、今まで見てきた放物線と違っていて少し気持ち悪いですね。横に寝ていますからね。今まで見たように、 y 軸を軸とする放物線ならどうなるかを考えてみましょう。

これは、上の例題で見た内容で、 $x,y$ をすべて入れ替えればOKです。そうすると、 $p\ne0$ のとき、焦点が $(0,p)$ で、準線が $y=-p$ の放物線が $x^2=4py$ となることがわかります。書き換えれば、 $y=\dfrac{1}{4p}x^2$ ということですね。

今まで、放物線は二次関数のグラフとして扱ってきました。 $y=ax^2$ のグラフ、というような具合ですね。 $a=\dfrac{1}{4p}$ とおけば、この放物線の焦点は $\left(0,\dfrac{1}{4a}\right)$ で、準線は $y=-\dfrac{1}{4a}$ となることがわかります。

今まで見てきた二次関数のグラフと、上で見た内容は、このような関係式でつながっています。

おわりに

ここでは、放物線の図形的な定義を見てきました。また、その定義に出てくる、焦点と準線についても見てきました。ここで出てくる「焦点」がなぜ焦点というかは、また別の機会に見ていくことにしましょう。