【基本】平均値・中央値・最頻値はどう使い分ける?
主なデータの代表値に、平均値、中央値、最頻値の3つがあります。どれも、データ全体の特徴を表すものですが、どうして代表値が3つもあるのでしょうか。「1個なら覚えるのも楽なのに!」と言いたい人もいるでしょう。また、結局どれを使えばいいのかわからないという人もいるかもしれません。
ここではそういった疑問について考えていきます。3つの代表値のメリット・デメリットや、使い分けについて考えていきます。
各代表値の得意・不得意
代表値とは、データ全体の特徴を表した値のことです。平均値は、「すべての数値を足して、数値の個数で割ったもの」、中央値は、「数値を小さい方から並べたときに、真ん中に来るもの」、最頻値は、「一番個数が多いもの」です。どれも「データを特徴づける値」ですが、それぞれの代表値には、得意・不得意があります。
データが次のようにきれいな左右対称の山の形に分布していた場合は、平均値も中央値も最頻値も等しくなります。
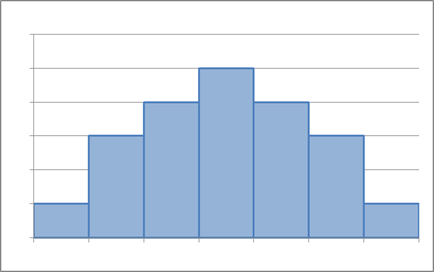
問題は非対称の場合です。次のような場合には、平均値・中央値・最頻値が等しくなるとは限りません。
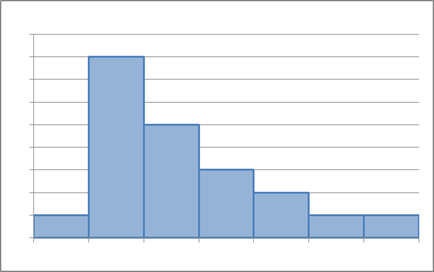
平均値は、すべての数値が計算式の中に出てくるので、「データを代表している」感が強く、よく使われます。しかし、逆にいうと、平均値には「極端な数値があった場合、それも考慮してしまう」というデメリットがあります。【基本】データの中央値#平均値の欠点でも紹介しましたが、大きすぎる値・小さすぎる値が含まれると、平均値はその影響を大きく受けてしまいます。
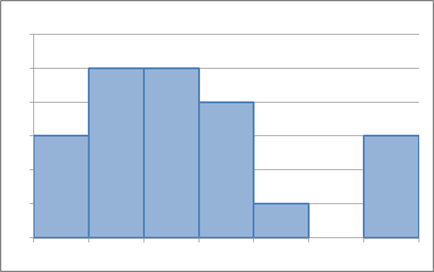
例えば、年収200万円の社員9人のところに、年収8200万円の社員が加われば、平均年収は1000万になります。しかし、「社員の平均年収が1000万」と聞いてこの会社に入った人がいたとすれば、きっと入社後には「思ってたのと違う!」と言うことでしょう。
一方、中央値や最頻値は、大きすぎる値や小さすぎる値がいくつか含まれていたとしても、ほとんど影響を受けません。中央値は、上から数えても下から数えても同じ順位の数値なので、上位・下位に極端な値があっても無視されます。最頻値も、例外的な値は無視されます。
では、平均値を使わずに、いつも中央値や最頻値を使えばいいじゃないか、と思うかもしれません。しかし、これもなかなか難しいんですね。
中央値は、データ全体ではなく、ピンポイントで真ん中だけを表しているので、データ全体の変化や比較には向かないことがあります。
例えば、ある3人のテストの結果が、50点、70点、90点だったとしましょう。次のテストで、90点の人が100点をとったとしても、他の2人が変わらなければ、中央値は変わりません。この場合に中央値を見て「テストの点数は変わらなかった」と分析されると、高得点をとった人は報われません。
また、3人の次のテストの結果が、30点、75点、80点になったとしましょう。真ん中以外の点数が下がっても、真ん中の人の点数が上がったため、中央値はあがります。この場合に中央値を見て「テストの点数は上がった」と分析するのもおかしいです。
このように、中央値が適さない場面があります。
最頻値は、データ数が多い場合でしか使えない、という欠点があります。極端な話、どの値も1回しか出てこないのであれば、「一番個数が多いもの」は意味を成しません。
データ数が少ない場合や同じ数値が少ない場合は、範囲で区切って集計する方法もあります。しかし、範囲をどう区切るかを決めるのも簡単ではありません。
例えば、ある11人のテストの点数が次の通りだったとしましょう。全員81点以上だったとします。
| 点数 | 人数 |
|---|---|
| 96-100 | 4 |
| 91-95 | 1 |
| 86-90 | 3 |
| 81-85 | 3 |
上のように5点刻みなら、データが一番多い区間は「96~100点」です。しかし、10点刻みにすると「81~90点」の方が多くなってしまいます。「96~100点」を含む区間が一番多いというわけではありません。区切り方によって、一番多い区間は変わってきます。このように、最頻値には、区間をどうわけるかによって値が変わる可能性があるという問題もあります。これでは、恣意的な結果が選ばれてしまうかもしれません。
つまり、どの代表値にも、いい面といまいちな面もある、ということです。
どの代表値を選べばいいか
代表値は「たくさんある数値の特徴を1つの数値で表す」というものであり、そもそもこれだけですべてを表すのには無理があります。1つの数値で表現できれば楽ですが、分布の仕方がきれいでない場合は、逆に誤解を招くおそれもあります。
このことを踏まえたうえで、それぞれの値の特徴を考慮して、次のように使うのがいいでしょう(使い方の一例です)。
基本的には、平均値と中央値を見比べて、大きくずれていなければ平均値を使う、という方針でいいでしょう。この2つが大きくずれていなければ、「きれいに分布している」ことが多いからです(いつもきれいだとは言えませんが)。
もしこの2つが乖離していれば、分布に偏りがあるということなので中央値を見る、大きく乖離していれば最頻値も見る、という順番がいいと思います。
ただ、繰り返しになりますが、分布が偏っている場合には、「代表値という1つの数値で全体を表す」ことが無謀である可能性があります。例えば、山が2つあるような場合に、1つの数値で分布を表してしまうと、逆に大事な情報が落ちてしまいます。
代表値の特徴を把握したうえで、今行おうとしている分析に適しているかどうかを判断しなければいけません。場合によっては、代表値を使う意味がないこともあります。そういう場合は、散らばりを表す箱ひげ図や分散、もしくはヒストグラムを使うことも検討しましょう。
おわりに
平均値・中央値・最頻値について、見てきました。もう一度、メリット・デメリットをまとめておきます。
メリット :すべての値が反映される
デメリット:極端な値があった場合に大きく影響を受ける
【中央値】
メリット :極端な値の影響を受けづらい
デメリット:データ全体の変化や比較には向かないこともある。
【最頻値】
メリット :極端な値の影響を受けづらい
デメリット:個数が少ない場合は使えない。区間の幅によって結果が変わることもある。
これらを踏まえて、今分析しているデータがどう分布しているかを見て、どれを使うかを考えるようにしましょう。





