【基本】対数
ここでは、対数の基本的な考え方について見ていきます。
対数とは何か
【標準】指数の計算というページで次のような問題を見ました。\[ 2^{\frac{1}{2} }\times 32^{\frac{1}{6} }\div 8^{\frac{1}{9} } \]これは、まず「2のなんとか乗」の形にしてから計算するのでした。
\begin{eqnarray}
& &
2^{\frac{1}{2} }\times 32^{\frac{1}{6} }\div 8^{\frac{1}{9} } \\[5pt]
&=&
2^{\frac{1}{2} }\times (2^5)^{\frac{1}{6} }\times (2^3)^{-\frac{1}{9} } \\[5pt]
&=&
2^{\frac{1}{2}+\frac{5}{6}-\frac{3}{9} } \\[5pt]
&=&
2^{\frac{3+5-2}{6} } \\[5pt]
&=&
2
\end{eqnarray}さて、この計算をよく見てみましょう。計算が行われているメインの場所はどこでしょうか。それは、2の右上の部分、指数の部分、ですね。分数で表して、通分して…、という計算を行っています。
しかし、文字の大きさでいうと、すごく小さいですね。小さい文字でちまちまと分数の計算をするのは大変です。しかも、2の部分は、「2のなんとか乗」で表した後は、計算上、あまり重要じゃないですね。2行目以降、ずっと変わりません。
こうしてみると、この計算で大きく取り上げたいのは指数の部分で、2の部分(底)はそんなに大きく取り上げる必要はないですね。このように、指数の部分に注目したいという場合に使えるのが、対数(logarithm) というものです。
具体的な例 $2^3=8$ を使って、対数の説明をしましょう。このとき、今までは、「2を3回掛けると、その結果は8」というふうに考えていました。対数の世界では、「2を何回掛けると8になるか、その答えは3」と考えます。指数の部分に着目したいために、こういう考え方になります。 $2^3=8$ を対数の言葉を使って書くと、「 $2$ を底(てい)とする $8$ の対数は、 $3$ である」となります。
では、「 $3$ を底とする $81$ の対数は?」と言われたらどうでしょうか。これは、「3を何乗したら81になるかな?」と考えればいいわけです。 $3^4=81$ となるので、対数は $4$ だ、ということがわかります。
慣れるまでは、なかなか難しいです。
対数を表す記号
先ほど、「 $2$ を底とする $8$ の対数は、 $3$ である」と書きましたが、毎回「 $2$ を底とする $8$ の対数」と書くのは面倒ですね。対数は、次のような記号で表します。\[ \log_2 8 =3 \]この左辺は、「 $2$ を底とする $8$ の対数」という意味です。 $\sin$ や $\cos$ のように、3文字まとめたものを1つの記号として扱います。対数は英語で logarithm というのですが、 $\log$ はそこから来ています。
「 $3$ を底とする $81$ の対数は、 $4$ である」というのは、\[ \log_3 81=4 \]となります。また、他にもいろいろ書いてみると、次のような式が成り立ちます。
\begin{eqnarray}
& 5^2=25 & \rightarrow & \log_{5} 25 = 2 \\[5pt]
& 5^\frac{1}{2}=\sqrt{5} & \rightarrow & \log_{5} \sqrt{5} = \frac{1}{2} \\[5pt]
& 8^\frac{1}{3}=2 & \rightarrow & \log_{8} 2 = \frac{1}{3} \\[5pt]
& 10^{-1}=\dfrac{1}{10} & \rightarrow & \log_{10} \dfrac{1}{10} = -1 \\[5pt]
\end{eqnarray}
ここまでのことをまとめておきましょう。
この $M$ のことを真数といいます。
真数条件
$a\gt 0, a\ne 1$ とします。 $a^p=M$ が成り立つとき、 $p$ は $a$ を底とする $M$ の対数というのでした。ここで、 $M$ がどんな値のときに対数が存在するのか、考えてみましょう。
【基本】指数関数の性質で見たように、指数関数 $y=a^x$ のグラフは、 $a$ の値によって形が大きく変わります。 $a\gt 1$ のときは次のようになります。
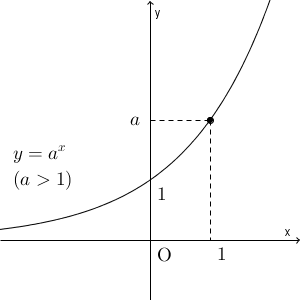
また、 $a\lt 1$ のときは、次のようになります。
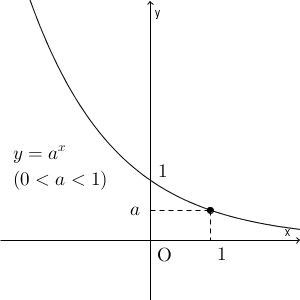
どちらの場合も、 $y=a^x$ は正の実数値すべてをとります。しかも、2か所で同じ値になることはありません。なので、 $M$ が正のときは、 $a^p=M$ となる $p$ がただ1つだけ存在します。
なので、 $a\gt 0, a\ne 1$ であり、 $M\gt 0$ なら、 $M$ が具体的にどんな値かわからなくても、 $a^p=M$ となる $p$ が存在するので、\[ \log_a M \]を考えることができる、というわけです。
例えば、 $\log_2 3$ というのは、「2を何乗すると3になるか」の答えを表していますが、具体的にどのような値なのかはパッとはわかりません。しかし、真数が正なので、このような対数も考えることは可能なんですね。
この「真数が正である」という条件は、対数を考える上での大前提となります。テキストや問題文で、 $\log_a M$ と書くと、 $M\gt 0$ という条件で考えることになります。この「真数が正である」という条件を、「真数条件」と呼ぶこともあります。
おわりに
ここでは、対数とは何か、対数を表す記号、について見てきました。慣れるまでは混乱しやすい内容ですが、慣れてくると計算がしやすいことが理解できるようになってきます。





