🏠 Home / 数学II / 図形と方程式 / 軌跡

【基本】軌跡（距離の2乗の和と円）

🕒 2017/09/01 🔄 2023/05/01

ここでは、2点からの距離の2乗の和が一定である点の軌跡について考えていきます。

📘 目次

距離の2乗の和と軌跡

例題

2点 $\mathrm{ A }(1,0)$, $\mathrm{ B }(-1,0)$ からの距離の2乗の和が $10$ である点 P の軌跡を求めなさい。

【基本】軌跡では具体的な問題を見ていませんでしたが、ここでは具体的に軌跡を求めてみましょう。問題文には、「点が動く」とは書いていませんが、「条件を満たすように点が動いたときの、動いた跡の図形」と考えて求めていきます。

まず、条件を満たす点が、どういう図形上にあるか、を考えていきます。しかし、問題文を見ても、図形的に考えて答えを想像することは難しそうです。上の図を見れば答えは明らかですが、試験中にはこの図は見れませんしね。

こういう場合は、座標を使って、計算で考えていきます。具体的には、 P の座標を $(x,y)$ とおき、条件を満たすときに $x,y$ の間でどんな関係式が成り立つかを求めます。そうすれば、どんな図形かを求めることができます。

「2点 $\mathrm{ A }(1,0)$, $\mathrm{ B }(-1,0)$ からの距離の2乗の和が $10$ 」とあるので、これを式で表してみます。
\begin{eqnarray} \mathrm{ AP }^2+\mathrm{ BP }^2 &=& 10 \\[5pt] (x-1)^2+y^2+(x+1)^2+y^2 &=& 10 \\[5pt] x^2-2x+1+y^2+x^2+2x+1+y^2 &=& 10 \\[5pt] 2x^2+2y^2 &=& 8 \\[5pt] x^2+y^2 &=& 2^2 \\[5pt] \end{eqnarray}と変形できます。よって、条件を満たす点 P は、円 $x^2+y^2=2^2$ 上にあることがわかります。

さて、【基本】軌跡で見たように、ここで終わりではなく、逆に「この図形上の点が、条件を満たすか」を見ていく必要があります。余計なものは除かないといけないんですね。

しかし、上の計算を逆にたどっていけば、簡単に確かめられます。 $\mathrm{ P }(x,y)$ が $x^2+y^2=2$ を満たすのであれば、
\begin{eqnarray} x^2+y^2 &=& 2^2 \\[5pt] 2x^2+2y^2 &=& 8 \\[5pt] x^2-2x+1+y^2+x^2+2x+1+y^2 &=& 10 \\[5pt] (x-1)^2+y^2+(x+1)^2+y^2 &=& 10 \\[5pt] \mathrm{ AP }^2+\mathrm{ BP }^2 &=& 10 \\[5pt] \end{eqnarray}と変形できます。普通、このような複雑になっていく式変形はあまりしませんが、上で行った計算を逆にたどっていくだけなので難しくないですね。このような変形ができるため、条件「2点 $\mathrm{ A }(1,0)$, $\mathrm{ B }(-1,0)$ からの距離の2乗の和が $10$ 」を満たすことがわかります。なので、除かないといけない点は1つもありません。

以上から、求める軌跡は、「原点が中心で、半径が $2$ の円」であることがわかります。

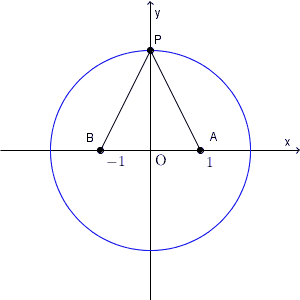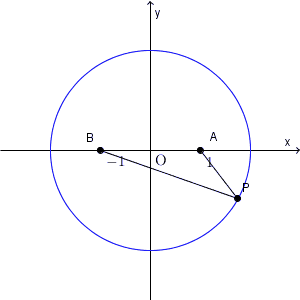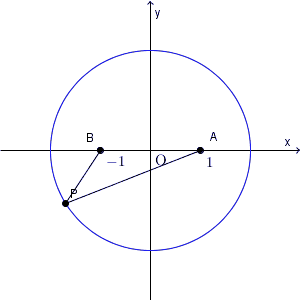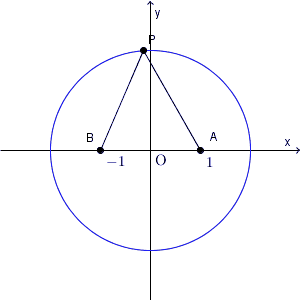
問題文を見ると、円を表しているようには感じられませんが、円になるんですね。「ある点から一定の距離だけ離れた点」以外にも、軌跡が円になるような条件があるんですね。

ここでは、後半部分で、説明のために逆にたどっていった式変形を書きましたが、試験などでは「逆に、円 $x^2+y^2=2$ 上の点 $\mathrm{ P }(x,y)$ について、 $\mathrm{ AP }^2+\mathrm{ BP }^2 = 10$ が成り立つ」と書く程度でも大丈夫でしょう。式変形が同値変形であれば、計算を逆にたどっていくことができるので、条件を満たすことがすぐにわかるからです。

除かないといけない点がある例は、今後見ていきます。

なお、この問題では答えは円となりましたが、「2点からの距離の2乗の和が一定」となる点の軌跡が円になるとは限りません。今回はたまたま円になるように、点や数字が選ばれています。