【基本】軌跡(垂直二等分線や角の二等分線)
ここでは、軌跡が直線になるものを見ていきます。作図などで学んだものが、座標を使って表すとどうなるか、確認していきましょう。
平行な直線
図形的に考えれば、答えが何になるかは予想できると思いますが、座標を使った計算ではどうなるかを見ていきましょう。
与えられた直線の方程式は\[ 3x-4y=0 \]と変形できます。この直線と点 $(X,Y)$ との距離が $1$ だとします。 $(x,y)$ だと直線の方程式に出てくる文字と同じでまぎらわしいので、文字を変えています。【標準】点と直線との距離で見た内容から、
\begin{eqnarray}
\frac{|3X-4Y|}{\sqrt{3^2+(-4)^2} } &=& 1 \\[5pt]
|3X-4Y| &=& 5 \\[5pt]
3X-4Y &=& \pm 5 \\[5pt]
\end{eqnarray}となります。点 $(X,Y)$ がこの関係式を満たすことから、この点の軌跡は\[ 3x-4y+5=0,3x-4y-5=0 \]上にあります。逆に、この直線上の点が条件を満たすことは、上の計算を逆にたどっていけばわかるので、これが求める軌跡です。

直線からの距離が一定なので、答えは元の直線に平行な直線になります。
垂直二等分線
距離の比が一定の場合は、【基本】軌跡(距離の比と円)で見たように、1つの例外を除いて、円になります。例外は $1:1$ のときです。この例題がそのケースです。
上のリンク先と同じように、点 $(x,y)$ が条件を満たすとして式を作って変形していきます。
\begin{eqnarray}
x^2+y^2 &=& (x-2)^2+(y-2)^2 \\[5pt]
0 &=& -4x+4-4y+4 \\[5pt]
y &=& -x+2 \\[5pt]
\end{eqnarray}となります。計算を逆にたどれば、この直線上の点が条件を満たすことがわかるので、これが求める軌跡となります。
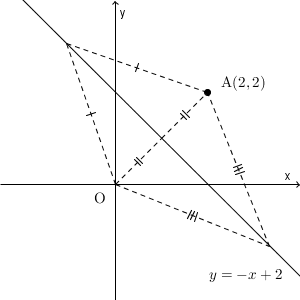
垂直二等分線ですね。
このように計算で求めてもいいですが、図形的に考えて「垂直二等分線になる」ということはわかるので、 OA の中点を通り、 OA に垂直な直線の方程式を求める方法でも構いません。
中点は $(1,1)$ であり、 OA の傾きは $1$ だから、これに垂直な直線の傾きは $-1$ です。よって
\begin{eqnarray}
y-1 &=& -(x-1) \\[5pt]
y &=& -x+2 \\[5pt]
\end{eqnarray}と求めることもできます。
角の二等分線
「2直線からの距離が等しい」ということは、「2直線のなす角の二等分線」ということですね。
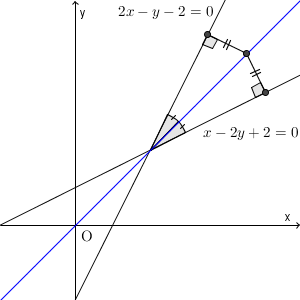
図形的に考えれば答えは「角の二等分線だ」ということはわかりますが、それがどんな傾きの直線になるかはわかりづらいですね。先ほどの「垂直二等分線」のときの後半部分とは、少し状況が違います。角の二等分線は、計算で考えていくのがいいでしょう。
点 $(X,Y)$ が条件を満たすとします。【標準】点と直線との距離で見た内容から、
\begin{eqnarray}
\frac{|X-2Y+2|}{\sqrt{1^2+(-2)^2} } &=& \frac{|2X-Y-2|}{\sqrt{2^2+(-1)^2} } \\[5pt]
|X-2Y+2| &=& |2X-Y-2| \\[5pt]
X-2Y+2 &=& \pm (2X-Y-2) \\[5pt]
\end{eqnarray}となります。 $X-2Y+2 = 2X-Y-2$ のときは
\begin{eqnarray}
-Y &=& X-4 \\[5pt]
Y &=& -X+4 \\[5pt]
\end{eqnarray}となり、 $X-2Y+2 = -(2X-Y-2)$ のときは
\begin{eqnarray}
3X-3Y&=&0 \\[5pt]
Y&=&X \\[5pt]
\end{eqnarray}となります。よって、軌跡は\[ y=-x+4, y=x \]上にあることがわかり、計算を逆にたどればこれらの直線上の点は条件を満たすことがわかるので、これらが求める軌跡となります。
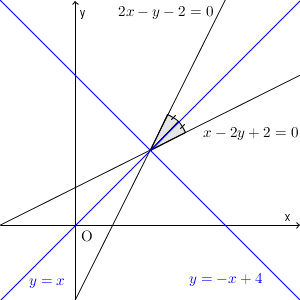
なす角は1つだけではないため、角の二等分線も1本ではありません。2本あります。気をつけましょう。
おわりに
ここでは、平行な直線、垂直二等分線、角の二等分線が求める軌跡となる例を見てきました。答えが予想できるので、それらを計算でどのように導くかを見れば、軌跡を求める手順が理解しやすいと思います。直線の方程式などで $x,y$ が使われている場合には、条件を満たす点を $(x,y)$ ではなく $(X,Y)$ などとおくことにも気をつけましょう。





