【基本】軌跡（距離の比と円）

🕒 2017/09/02 🔄 2023/05/01

ここでは、ある点が、2つの定点からの距離の比が一定となるように動いたときの軌跡について考えます。

📘 目次

距離の比と軌跡

例題

原点からの距離と $\mathrm{ A }(3,0)$ からの距離の比が $2:1$ である点 P の軌跡を求めなさい。

【基本】軌跡（距離の2乗の和と円）のときと同じように、点 P の座標を $(x,y)$ とおいて、関係式を考えていきましょう。

まず、原点からの距離は、 $\sqrt{x^2+y^2}$ となりますね。 A からの距離は、 $\sqrt{(x-3)^2+y^2}$ です。この比が $2:1$ と一定であることから、次の式が成り立ちます。
\begin{eqnarray} \sqrt{x^2+y^2}:\sqrt{(x-3)^2+y^2} &=& 2:1 \\[5pt] \sqrt{x^2+y^2} &=& 2\sqrt{(x-3)^2+y^2} \\[5pt] \end{eqnarray}両辺は正なので、2乗して計算していくと \begin{eqnarray} x^2+y^2 &=& 4(x^2-6x+9)+4y^2 \\[5pt] 3x^2-24x+36+3y^2 &=& 0 \\[5pt] x^2-8x+12+y^2 &=& 0 \\[5pt] (x-4)^2+y^2 &=& 2^2 \\[5pt] \end{eqnarray}となります。よって、 P はこの円周上にあります。また、上の計算を逆にたどっていけば、この円周上にある点が条件を満たすこともわかります。

よって、求める軌跡は、「 $(4,0)$ を中心とする半径 $2$ の円」となります。

アポロニウスの円

上の例題では、距離の比が $2:1$ の場合を考えましたが、実は他の場合でも答えは円になります。2つの点 A, B があって、 $\mathrm{ AP }:\mathrm{ BP }=m:1$ となるように P が動くとします（ただし、 m は $1$ 以外の正の実数）。このとき、 P の軌跡は円になります。

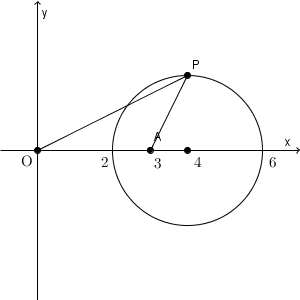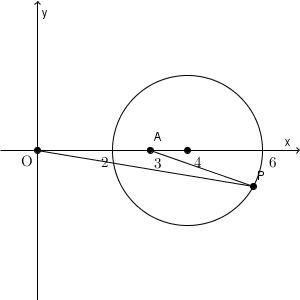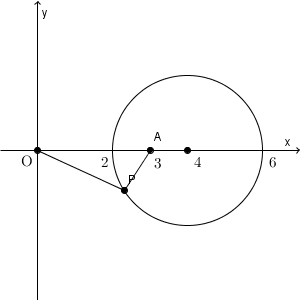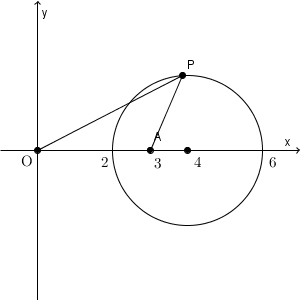
下の図は、 $\mathrm{ AP }:\mathrm{ OP }=m:1$ の m を動かしたときに、 P の軌跡がどのように変化するかを表したものです。大きさは変わりますが、円であることは変わりません。

この円のことを、アポロニウスの円(circles of Apollonius) と言います。なお、比が $1:1$ のときは、 P の軌跡は垂直二等分線となります。

このことを知っておけば、答えをあらかじめ予想しておくことができます。答えが円だとわかっていれば、あとは中心と半径が分かればいいですね。この円は、内分点と外分点を通ることは明らかで、この2点をつないだものが直径となります。なので、内分点と外分点の中点が円の中心、距離の半分が半径となります。

実際、上の例題も、原点と $(3,0)$ とをつないだ線分を $2:1$ に内分する点は $(2,0)$, 外分する点は $(6,0)$ なので、中心は $(4,0)$, 半径は $2$ であることがわかります（参考：【基本】平面上での内分点と外分点）。上で求めた答えと合っていますね。

ただし、これはあくまでも答えの予想です。実際の試験で、「距離の比が一定となるように動いたときの点の軌跡を求めなさい」といわれたら、アポロニウスの円のことは使わずに、上の例題で見たような解答を書かないといけません。「軌跡が円となることを示す」のが、試験問題の意図と考えられるからです。「アポロニウスの円」については、答えの予想として使いましょう。