【基本】二次関数y=ax^2+qのグラフ

【基本】二次関数 y=ax^2 のグラフでは、二次関数 $y=ax^2$ のグラフを見ました。ここでは、この二次関数のグラフを上下に移動したものを考えていくことにします。

平行移動

ある図形を、同じ方向に同じ距離だけ動かすことを平行移動(translation)といいます。例えば、下の三角形Bは三角形Aを平行移動したものです。

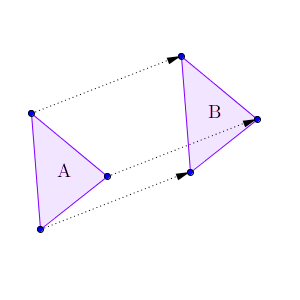
移動前と移動後の点を結ぶと、どれも互いに平行になります。上の図でも、各矢印が平行になっていることが分かります。なので、このような移動を「平行移動」と呼ぶのは自然でしょう。

回転したり、左右が反転したものは平行移動とはいいません。また、一部だけが平行移動していてもダメです。図形全体が同じ方向に同じ距離だけ動いた場合だけ「平行移動」といいます。

点の移動

最終的には、二次関数 $y=ax^2+bx+c$ のグラフを考えるのですが、いきなり考えるのは難しいです。しかし、簡単なケース $y=ax^2$ から出発して（参考：【基本】二次関数 y=ax^2 のグラフ）、このグラフを平行移動する、という順番で考えると、一般的なケースでも対応できるようになります。

グラフの平行移動を考えていく前に、まずは、点の移動について見ていきましょう。

点の移動について、数学では次のような言い方をします。

「点 $\mathrm{ A }(1,2)$ を x 軸方向に $2$ 、y 軸方向に $-1$ に移動した点を B とする。」

x 軸方向とは、x 軸の正の方向、つまり、「右」ということです。そのため、これは「x 軸の正の方向（＝右方向）に $2$ 移動する」「y 軸の負の方向（＝下方向）に $1$ 移動する」ことになります。

図をかくと、次のようになります。

移動後の点 B の座標はどうなるでしょうか。これは単に移動距離を足すだけで求められます。負の方向に移動する場合は、負の数を足します。\[ (1+2,2-1) \]なので、 $(3,1)$ となります。図ともあっていますね。

わざわざ書くほどのことでもないかもしれませんが、一般的に次のことが成り立ちます。

二次関数 y=ax^2+q のグラフ

さて、二次関数のグラフの話に戻りましょう。ここでは、二次関数 $y=ax^2$ のグラフを y 軸方向に動かす場合を考えます。平行移動した後のグラフは、どんな関数のグラフになっているでしょうか。

例として $y=x^2$ のグラフを y 軸方向に $2$ だけ移動したものを考えてみましょう。グラフをかくと、次のようになります。

グレーが移動前、黒い太線が移動後のグラフです。各点の移動に注目して、具体的な点の座標をいくつか書いてみます。下の表の y は、新しいグラフでの y 座標を表しています。

\begin{array}{c | rrrrrrr } x & \cdots & -2 & -1 & 0 & 1 & 2 & \cdots \\ \hline x^2 & \cdots & 4 & 1 & 0 & 1 & 4 & \cdots \\ \hline y & \cdots & 6 & 3 & 2 & 3 & 6 & \cdots \end{array}

移動前の点の y 座標（上の表の2段目）に $2$ を加えたものが、新しいグラフ上の点の y 座標となります。このことから、移動後のグラフに対応する新しい関数は $y=x^2+2$ であることがわかります。上の黒い太線のグラフが $y=x^2+2$ のグラフということです。

逆に、関数 $y=x^2+2$ からグラフを考えてみましょう。

このグラフ上の点 $(x,x^2+2)$ は、点 $(x,x^2)$ を y 軸方向に $2$ だけ移動したものです。これが、すべての x について成り立つので、「 $y=x^2+2$ のグラフは、 $y=x^2$ のグラフを y 軸方向に $2$ だけ平行移動したもの」ということができるんですね。

一般的に、次のことがいえます。

【基本】二次関数 y=ax^2 のグラフでは、放物線の頂点と軸の紹介をしました。二次関数 $y=ax^2+q$ については、上の図からもわかる通り、軸は y 軸、頂点の座標は $(0,q)$ となります。

もう一つの例

もう一つ例を挙げておきます。二次関数 $y=-2x^2+2$ のグラフをかいてみます。まず $y=-2x^2$ を考えて、それを y 軸方向に $2$ だけ平行移動すればいいですね。

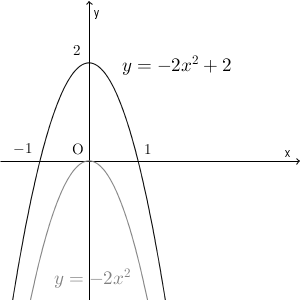
グレーの放物線は、移動前のものなので、かく必要はありません。y 軸との交点の座標は、 $x=0$ とすれば求められますね。グラフをかくときには一緒に書いておきましょう。x 軸との交点は、わかる場合は書いたほうがいいのですが、これについては、求め方も含めて、【基本】二次関数のグラフとx軸との共有点で詳しく見ていきます。

なお、この放物線の軸は y 軸、頂点の座標は $(0, 2)$ となります。

おわりに

ここでは、二次関数 $y=ax^2+q$ のグラフについて見てきました。このグラフのかき方は、次のようになります。

• 頂点 $(0,q)$ を把握し、座標を書く
• 頂点をもとに、放物線をかく
• 放物線上のどこか1点の座標を書く

放物線上のどこか1点の座標を書くのは、放物線が特定できるようにするためです。【基本】二次関数 y=ax^2 のグラフでも見た通り、放物線には鋭いものや広がっているものがあるため、特定できるようにする必要があります。 $x=1$ のときなどの座標を追加するか、x 軸との交点の座標を追加くようにしましょう。

次は左右に平行移動した場合を見ていきます。