【基本】二次関数y=a(x-p)^2+qのグラフ
【基本】二次関数y=ax^2+qのグラフ と 【基本】二次関数y=a(x-p)^2のグラフ で、関数 $y=ax^2$ のグラフを x 軸方向に動かした場合、y 軸方向に動かした場合を見てきました。ここでは、同時に動かす場合を考えてみます。
といっても、2つの内容を合わせるだけです。
二次関数y=a(x-p)^2+qのグラフ
関数 $y=2x^2$ のグラフを、x 軸方向に $2$ 、y 軸方向に $1$ だけ動かしたグラフを考えましょう。
まず、【基本】二次関数y=a(x-p)^2のグラフで見たように、関数 $y=2x^2$ のグラフを、x 軸方向に $2$ 動かしたものは、 $y=2(x-2)^2$ のグラフになります。グラフを $+p$ 動かすと、式には $-p$ が出てくるんでしたね。
さらにこれを y 軸方向に動かすと、【基本】二次関数y=ax^2+qのグラフの内容と同じように考えれば、移動後のグラフは $y=2(x-2)^2+1$ のグラフになることが分かります。

右辺を展開すると、 $2x^2-8x+9$ になるので、上のグラフは $y=2x^2-8x+9$ のグラフであるともいえます。
また、 $y=2(x-2)^2+1$ からグラフを考えてみると、 $y=2x^2$ を x 軸方向に $2$ 、y 軸方向に $1$ だけ動かしたグラフだということも、今までと同じように考えればわかります。
なお、移動後の放物線の軸は $x=2$ 、頂点の座標は $(2,1)$ となります。
一般的に次が成り立ちます。
移動後の放物線の軸は $x=p$ 、頂点の座標は $(p,q)$ となります。
どうしてpとqの符号が違うのか
$y=ax^2$ のグラフを x 軸方向に p 、 y 軸方向に q だけ移動したものは、 $y=a(x-p)^2+q$ のグラフになる、ということを見てきましたが、なぜ p と qの符号は違うのでしょう。少し難しいですが、考えていきましょう。(難しい場合は飛ばしてもいいです)
移動前のグラフ上の点を、 $(X,Y)$ とおいてみます。これは $y=ax^2$ のグラフ上の点なので、\[ Y=aX^2 \]が成り立ちます。移動後の点を $(x,y)$ とおくと、移動内容から\[ (X+p, Y+q) = (x,y) \]が成り立つことが分かります。これは次のようにも書き換えることができます。\[ (X,Y) = (x-p,y-q) \]ここではじめに書いたように $Y=aX^2$ が成り立つので、代入すると\[ y-q = a(x-p)^2 \]が得られるんですね。
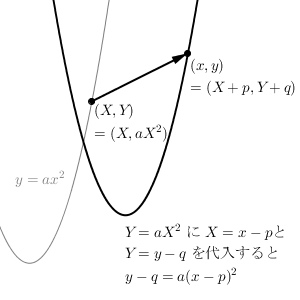
つまり、移動前の式で x を $x-p$ に、y を $y-q$ に置き換えたものが、移動後のグラフの式になる、ということです。具体的に書くと\[ y-q=a(x-p)^2 \]になります。
これを移行すれば $y=a(x-p)^2+q$ になります。p と q の符号が違うようにも見えますが、本当は両方とも符号はマイナスだったんですね。 $-q$ を右辺に移行してきたので $+q$ となり、 $p$ と符号が違うように見えていただけです。
おわりに
ここでは、二次関数 $y=a(x-p)^2+q$ のグラフについて見てきました。このグラフのかき方は、次のようになります。
- 頂点 $(p, q)$ を把握し、座標をかく
- 頂点をもとに、放物線をかく
- 軸との共有点の座標やグラフ上のある1点の座標をかく
3つ目は、放物線を特定するために必要なものですね。
さて、ここまでで $y=ax^2$ のグラフを平行移動して $y=a(x-p)^2+q$ の形になる二次関数のグラフがどうなるかを見てきました。しかし、実際には $y=ax^2+bx+c$ のグラフをかくことが多いんですね。次はこの形の二次関数のグラフについて、見ていくことにします。





