【基本】二次関数y=a(x-p)^2のグラフ

🕒 2016/07/12 🔄 2023/05/01

【基本】二次関数y=ax^2+qのグラフでは、二次関数 $y=ax^2$ のグラフを y 軸方向に移動した場合を考えました。ここでは、x 軸方向に移動した場合を考えていきます。

📘 目次

二次関数y=a(x-p)^2のグラフ

例として、 $y=x^2$ のグラフを x 軸方向に $1$ だけ移動したものを考えてみます。グラフは次のようになります。

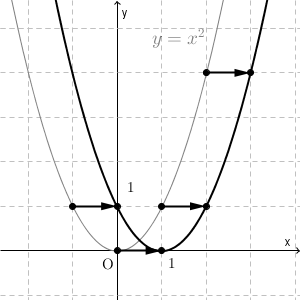
グレーが移動前、黒い太線が移動後のグラフです。各点の移動に注目して、グラフを見ながら点の座標をいくつか書いてみます。移動前は次のように対応しています。
\begin{array}{c | rrrrrrr } x & \cdots & -1 & 0 & 1 & 2 & 3 & \cdots \\ \hline x^2 & \cdots & 1 & 0 & 1 & 4 & 9 & \cdots \end{array} 移動後はこうなります。 y は、新しいグラフでの y 座標を表しています。
\begin{array}{c | rrrrrrrr } x & \cdots & -1 & 0 & 1 & 2 & 3 & 4 & \cdots \\ \hline y & \cdots & 4 & 1 & 0 & 1 & 4 & 9 & \cdots \end{array} 移動前の点の y 座標（1つ目の表の2段目）を1つ右にずらしたものが、新しいグラフ上の点の y 座標となります。逆に言うと、新しいグラフ上の点を1つ左にずらせば、移動前のグラフに戻るということです。

新しいグラフ上の点を $(x,y)$ とすると、この1つ左の点は $(x-1,y)$ です。この点は移動前のグラフ上の点なので、x 座標を2乗すると y 座標と等しくなります。つまり、 $y=(x-1)^2$ が成り立ちます。これが、新しいグラフに対応する関数となります。

実際に上の表で $y=(x-1)^2$ が成り立っていることは、それぞれ計算してみると確かめることができます。

逆に、関数 $y=(x-1)^2$ から、グラフを考えてみましょう。

このグラフ上の点 $(x,(x-1)^2)$ は、点 $(x-1,(x-1)^2)$ を x 軸方向に $1$ だけ移動したものです。点 $(x-1,(x-1)^2)$ は、x 座標を2乗すると y 座標となるので、 $y=x^2$ のグラフ上の点です。

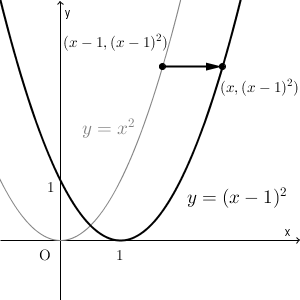
このような点の対応が、すべての x について成り立つので、「 $y=(x-1)^2$ のグラフは、 $y=x^2$ のグラフを x軸方向に $1$ だけ平行移動したもの」ということができます。

x 軸方向に $1$ 移動すると言っておいて、 $x+1$ ではなく $x-1$ が出てくるので、はじめは不思議に思うかもしれません。「新グラフから反対に移動すると、元の関数のグラフになる」ことから、マイナスが出てくる、と考えましょう。

なお、この放物線の頂点の座標は $(1,0)$ で、軸は $x=1$ となります。グラフ全体が $x$ 軸方向に $1$ 移動しているので、頂点も軸も x 軸方向に $1$ ずれます。

一般的に、次が成り立ちます。

$y=a(x-p)^2$ のグラフ

$y=a(x-p)^2$ のグラフは、 $y=ax^2$ のグラフを x 軸方向に p だけ移動したものである

この放物線の頂点の座標は $(p,0)$ で、軸は $x=p$ となります。

もう一つの例

もう一つ例を見てみましょう。

$y=-2(x+1)^2$ のグラフを考えます。

このグラフ上の点は、 $(x,-2(x+1)^2)$ と表すことができます。これを x 軸方向に $1$ 動かせば、 $(x+1,-2(x+1)^2)$ となります。この点の $y$ 座標は、 $x$ 座標を2乗して $-2$ を掛けたものと一致するので、この点は $y=-2x^2$ のグラフ上にあることがわかります。

つまり、「x 軸方向に $1$ 動かせば $y=-2x^2$ のグラフ上に来る」ということなので、「 $y=-2x^2$ のグラフをx軸方向に $-1$ 動かせば、考えたいグラフになる」ということです。そのため、グラフは次のようになります。

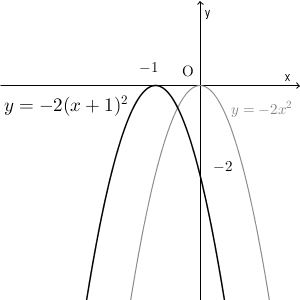
グレーの放物線は、移動前のものなので、かく必要はありません。y 軸との交点の座標は、 $x=0$ とすればすぐに求められるので、グラフをかくときには一緒に書いておきましょう。なお、この放物線の軸は $x=-1$ 、頂点の座標は $(-1, 0)$ となります。

どっちに動かせばいいかわからない場合

$y=a(x-p)^2$ のグラフは、 $y=ax^2$ のグラフを x 軸方向に p だけ移動したものですが、どっちに動かせばいいか忘れてしまったとか、なかなか理解できない、という場合があるかもしれません。

そういうときは、カッコの中が $0$ になる場合を考えましょう。

カッコの中が0になるところが、放物線の軸になります。 $y=a(x-p)^2$ という式なら、 $x=p$ のときにカッコの中が $0$ になります。 $x=p$ を中心に考えると、左右対称になることがわかるので、これが軸です。軸がわかれば頂点もわかるので、あとはこの頂点をもとに、放物線をかけばいいんですね。

上で見た例であれば、 $y=(x-1)^2$ は $x=1$ のときにカッコ内が $0$ になるので、軸が $x=1$ だとわかります。なので、 $(1,0)$ を頂点としてグラフをかけばいいです。 $y=-2(x+1)^2$ の場合も同様に考えると、 $x=-1$ が軸になることがわかります。

こうすれば、右に動かすか、左に動かすかを間違うことはないでしょう。