【基本】絶対値のついた二次関数のグラフ
ここでは、絶対値のついた二次関数のグラフをかく問題を見ていきます。
絶対値のついた二次関数のグラフその1
絶対値のついた関数のグラフをかくには、場合分けをして絶対値をはずすのが基本です。 $x^2-2x$ の符号に注目して、絶対値をはずします。
$x^2-2x\geqq 0$ を解くと $x(x-2)\geqq 0$ より、 $x\leqq 0, x\geqq 2$ となります。また、 $x^2-2x\lt 0$ となるのは $0\lt x \lt 2$ のときであることもわかります。
以上から、 $y=|x^2-2x|$ のグラフは次のようになります。
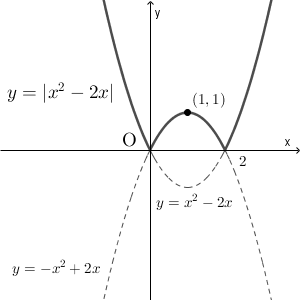
【基本】絶対値のついた一次関数のグラフでも見たように、 $y=|f(x)|$ の形の関数のグラフは $y=f(x)$ のグラフで $x$ 軸の下側を折り返したものになります。この例題でも、 $0\lt x\lt 2$ の範囲では、 $y=x^2-2x$ のグラフを折り返したものになっています。この問題では、「折り返し」を利用してグラフをかいても構いません。
絶対値のついた二次関数のグラフその2
今度は、全体ではなく $x$ の部分だけに絶対値がついています。このような場合には「折り返し」でグラフをかくことはできません。絶対値の中身に応じて場合分けをして考えていきます。
まず、 $x\geqq 0$ の場合は、絶対値の中身は0以上なので、次のように計算できます。
\begin{eqnarray}
y
&=&
x^2-2|x| \\[5pt]
&=&
x^2-2x \\[5pt]
&=&
(x-1)^2-1 \\[5pt]
\end{eqnarray}一方、 $x\lt 0$ の場合は、絶対値の中身は負なので、 $|x|=-x$ となります。なので、次のように計算できます。
\begin{eqnarray}
y
&=&
x^2-2|x| \\[5pt]
&=&
x^2+2x \\[5pt]
&=&
(x+1)^2-1 \\[5pt]
\end{eqnarray}これらをつなぎ合わせれば、 $y=x^2-2|x|$ のグラフになります。下のようになります。
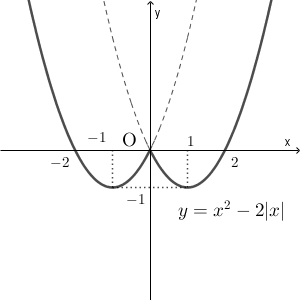
絶対値のついた二次関数のグラフその3
似たような式ですが、絶対値のついている箇所がまた違います。この場合も、式全体に絶対値がついているわけではないので、場合分けをして考えていきます。
このケースでは、 $x\geqq 2$ と $x\lt 2$ で場合分けをして考えていけばいいですね。 $x\geqq 2$ のときは
\begin{eqnarray}
y
&=&
x|x-2| \\[5pt]
&=&
x(x-2) \\[5pt]
&=&
(x-1)^2-1 \\[5pt]
\end{eqnarray}と変形でき、 $x\lt 2$ のときは
\begin{eqnarray}
y
&=&
x|x-2| \\[5pt]
&=&
-x(x-2) \\[5pt]
&=&
-(x-1)^2+1 \\[5pt]
\end{eqnarray}となります。範囲に応じてグラフをかいてつなぎ合わせると、次のようなグラフになることがわかります。
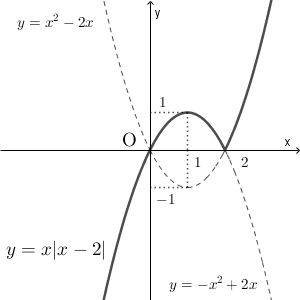
おわりに
ここでは、絶対値のついた二次関数のグラフをかく問題を見てきました。絶対値がどこにつくかでグラフの形は全然違ってきます。 $x$ の値で場合分けをしてグラフをかく、という基本を忘れないようにしましょう。





