【基本】二次関数 y=ax^2 のグラフ

🕒 2016/07/10 🔄 2023/05/01

ここから、二次関数のグラフについて見ていきます。まずは、とても基本的な $y=ax^2$ から見ていきます。

📘 目次

二次関数

x の二次式で表される関数を、二次関数(quadratic function)といいます。 $y=2x^2+x-3$ のような形の関数です。一般的な形で書くと、x の二次関数 y は、定数 a, b, c を用いて、次のように表すことができます。\[ y=ax^2+bx+c \]ただし、 $a\ne 0$ とします。 $a=0$ の場合には右辺が二次式にならないので、 $a=0$ のときは除きます。

二次関数 y=ax^2 のグラフ

二次関数 $y=ax^2+bx+c$ について調べるためには、このグラフがかけた方がいいのですが、どうやってかけばいいのでしょうか。まずは、 $y=ax^2$ の場合について、考えていくことにしましょう。

とてもシンプルな $y=x^2$ の場合を考えましょう。 $a=1$ のとき、ということです。この式に、 $x=0,1,2,3$ や $x=-1,-2,-3$ などの数字を入れていき、y の値を求めて点を記入していくと次のようになります。

目盛りの間隔は1です。

これをなめらかにつないだものが、 $y=x^2$ のグラフになります。

同じようにすれば、 $y=ax^2$ の形をしたほかの二次関数のグラフも次のようにかくことができます。ちょっとごちゃっとしていますが。

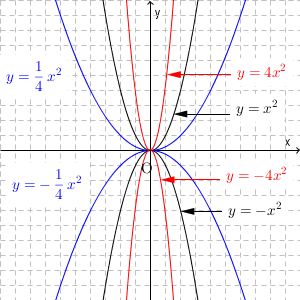
青いグラフが $\displaystyle y=\frac{1}{4}x^2$ と $\displaystyle y=-\frac{1}{4}x^2$ のグラフです。また、赤いグラフが $y=4x^2$ と $y=-4x^2$ のグラフです。

これらのグラフからわかるポイントは、次の通りです。

原点を通る
y 軸に関して、左右対称になっている
a が正なら x 軸の上、負ならx 軸の下
a の絶対値が大きくなるほど鋭くなり、小さくなると広がる

これらについて、もう少し詳しく見ていきましょう。

放物線、軸、頂点

上では、二次関数 $y=ax^2$ のグラフをいくつかかいてみました。これらの二次関数のグラフは、放物線(parabola)といいます。

上のグラフを見ると、鋭くなっていたり、広がっていたり、向きが違っていたり、いろんなパターンがあるように見えます。しかし、放物線はすべて相似で同じ形になっており、「物を放ったときにできる線」とも同じになります。今の段階でこれらのことを説明するのは難しいのでしませんが、これが二次関数のグラフを放物線と呼ぶ理由になっています。

上でまとめたポイントの中で、「y 軸に関して、左右対称になっている」というものがありました。これは式で考えると、 $x=p$ と $x=-p$ を代入して、どちらも $y=ap^2$ となることからわかります。これは、y 軸から同じ距離だけ離れた点の高さが同じであることを示しているからです。

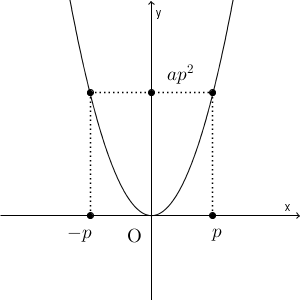
この線対称の軸のことを、放物線の軸(axis)といいます。なお、今後見ていくことになりますが、他の放物線でも、左右対称になることがいえます。

また、上でまとめたポイントの中で「原点を通る」というのもありました。どの二次関数も $x=0$ を代入すると $y=0$ となるからわかりますね。グラフを見ると、原点が谷の底や山の頂上になっていることがわかります。このような点を、放物線の頂点(vertex)といいます。頂点がどんな点かをもう少し正確に書くと、「放物線とその軸との交点」となります。

まとめると、 $y=ax^2$ のグラフは、「軸が y 軸で、原点が頂点の放物線」ということができます。

凸

最後に、上でまとめたポイントの中の「a が正なら x 軸より上、負なら x 軸より下」について見ていきます。

$y=ax^2$ は、 $x^2 \geqq 0$ なので、a が正なら x 軸の上にあることがわかります。x が増加していくとき、x が負なら y の値は下がっていき、x が正なら y の値は大きくなっていきます。その結果、グラフは谷のような形になります。

このように、下側に突き出たグラフのことを下に凸(とつ、convex downward)といいます。また、予想できると思いますが、 $a\lt 0$ のときのように、上に突き出たグラフのことを、上に凸(convex upward)といいます。山のような形になっているグラフのことですね。