【基本】関数のグラフ

ここでは、関数のグラフについて見ていきます。すでに知っている内容がほとんどだと思いますが、基本的なことなので復習のためにも見ておきましょう。

座標

日常生活では、言葉だけで説明するより図をかいて説明したほうがわかりやすいことがあります。数学でも同じで、数や式だけで考えるよりも、図にしたほうが状況が理解しやすくなることがあります。そんなときに使えるのがグラフです。

下のように、平面上に横軸（x 軸）と縦軸（y 軸）をかいたものを座標平面といいます。

グラフは、この座標平面上にかいていきます。

横軸と縦軸は、数直線と同じように、軸上の点と実数とが1つ1つ対応している、と考えます。右に行くほど、上に行くほど数字が大きくなります。このことを示すために、上の図でも右方向と上方向に矢印をかいています。また、2つの軸の交点 O は、原点といいます。

座標平面上にある点は、横軸・縦軸に下した垂線との交点に対応する「2つの数字」を使って表します。これを、その点の座標(coordinate)といいます。下の図の場合、点 P の座標は $(a,b)$ となります。

点が軸上にある場合は、軸上の数字を使って座標を考えます。例えば、上の例でいうと、P から x 軸に下した垂線と x 軸との交点の座標は $(a,0)$ となります。

点 P の座標が $(a,b)$ であることを、 $\mathrm{ P }(a,b)$ と表します。原点は $\mathrm{ O }(0,0)$ となります。

関数のグラフ

$y=2x-1$ のグラフのかき方はすでに学んでいるはずですが、もう一度考えてみましょう。

x の値を決めたとき、対応する y の値は次のようになります。

• $x=-1$ のとき $y=-3$
• $x=0$ のとき $y=-1$
• $x=1$ のとき $y=1$
• $x=2$ のとき $y=3$

これらを座標平面上で考えると、次のような4点になります。わかりやすいように、目盛りを入れています。

他の組合せについても同様に考えると、 $y=2x-1$ を満たす点 $(x,y)$ をとっていけば、次のようになります。

このように、関数 $y=f(x)$ が与えられたときに $(x,f(x))$ 全体で作られる図形を、この関数のグラフ(graph)と言います。上の例でいえば、 $f(x)$ は $2x-1$ ということですね。

「点 $(a,b)$ が関数 $y=f(x)$ のグラフ上にある」というのは、「 $b=f(a)$ が成り立つ」ことと同じことです。 $(x,f(x))$ 全体で作られる図形がグラフなんだから当たり前ですね。

このような対応があるので、「パッと見てどういう状況になっているか知りたい」というときにはグラフを見ればいいし、「厳密に値がどうなっているか知りたい」という場合には関数を使って計算すればいいわけです。

象限

最後に、言葉の紹介をして終わりにしましょう。

座標平面は、軸によって4つに分割されています。この1つ1つのパーツを、象限(しょうげん、orthant)といいます。また、それぞれに番号がついています。右上の部分を、第1象限といいます。そこから反時計回りに、第2象限、第3象限、第4象限といいます。

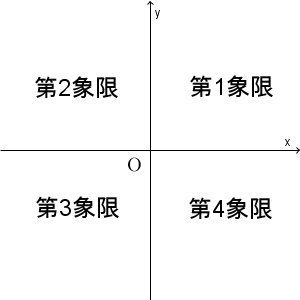
「右上が第1象限で、あとは反時計回り」ということだけ覚えておきましょう。入試問題で「ここは第何象限ですか？」みたいな問題は出ませんが、「第1象限に点Pをとる」というように、問題文中に使われることはあります。どこを指しているかはわかるようにしておきましょう。

なお、軸上の点は、どの象限にも含まれません。原点も、どの象限にも含まれません。

おわりに

ここでは、関数のグラフについて見てきました。ほとんどやったことのある内容だったと思いますが、「点 $(a,b)$ が関数 $y=f(x)$ のグラフ上にある」ことと「 $b=f(a)$ が成り立つ」ことが同じである、というのは重要です。これによってグラフと数式がつながるわけですね。